��Ŀ����
��֪����x�ķ�ʽ����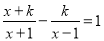 �Ľ�Ϊ��������k��ȡֵ��Χ��_________
�Ľ�Ϊ��������k��ȡֵ��Χ��_________
��x��y����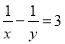 �����ʽ
�����ʽ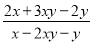 ��ֵΪ_________.
��ֵΪ_________.
����ѧ�ҷ���һ�ֲ����ij���ԼΪ0.000 043���ף��ÿ�ѧ��������ʾΪ_____��.
�鿴��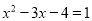 ��
�� 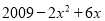 = _______
= _______
�����Ӽؿ����ҵ�,ÿСʱ��ʻ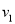 ǧ��,tСʱ�ɵ���.���ÿСʱ����ʻ
ǧ��,tСʱ�ɵ���.���ÿСʱ����ʻ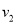 ǧ��,��ô������ǰ_______Сʱ���
ǧ��,��ô������ǰ_______Сʱ���
��ʽ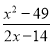 Լ�ֵĽ����_______
Լ�ֵĽ����_______
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
���壺��a+b=2�����a��b�ǹ���1��ƽ������
��1��3���� ���ǹ���1��ƽ������5��x���� ���ǹ���1��ƽ���������ú�x�Ĵ���ʽ��ʾ��
��2����a=2x2��3��x2+x��+4��b=2x��[3x����4x+x2����2]���ж�a��b�Ƿ��ǹ���1 ��ƽ��������˵�����ɣ�
��1����1��x��3����2��a��b���ǹ���1��ƽ���� �������������������1����ƽ�����Ķ��弴����ô𰸣� ��2������a+b�Ƿ����1���ɣ� �����������1����3�Ĺ���1��ƽ����Ϊa����3+a=2�����a=��1�� ��3�멁1�ǹ���1��ƽ������ ��5��x�Ĺ���1��ƽ����Ϊb����5��x+b=2�����b=2����5��x��=x��3�� ��5��x��x��3�ǹ���1��ƽ������ ...ij����һ�ܼƻ�ÿ���������г�100��,���ڹ���ʵ������,ÿ���ϰ�������һ�����,ʵ��ÿ����������ƻ������������±�(�Լƻ���Ϊ��,���ӵij�������Ϊ����,���ٵij�������Ϊ����):

��1������������һ������������ٵ�һ�������������?
��2�������ܵ��������Ƕ�����?
�鿴��ijһ���һ�������Թ�¥Ϊ�������ڶ�������Ӫ�ˣ�����Ϊ����������Ϊ�����г���̣���λ��ǧ�ף����Ⱥ�����¼���£�+9����3����5��+4����10��+6����3����6����4��+10
��1�������һ���˿��͵�Ŀ�ĵأ�������¥�������Զ���ڹ�¥��ʲô����
��2�������ÿǧ�ĺ�����Ϊ0.08������������������������������
�鿴���������ϱ�ʾ���и��������á���������������
��4����|��2.5|��������2����0����12��
�鿴���Ȼ�������ֵ��x2��3��2x2��4y��+2��x2��y������x=��2��y=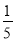 ��
��
����
��1����3xy��2y2+5xy��4y2
��2��2��5a2��2a����4����3a+2a2��
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
ij���ؼƻ��½�һ�����ε������أ�һ�߿���ǽ��ǽ�㹻�����������������ܳ�54�IJ����դ��Χ�ɣ���ǽƽ�е�һ����һ����Ϊ2�ij���ڣ���ͼ��ʾ�������Ʋ���ʹ�صĶ��������������λѧ��������龳��������������Ϣ��������⣺

��1����AB��x�ף�x��0�������ú�x�Ĵ���ʽ��ʾBC�ij���
��2�������ж�˭��˵����ȷ��Ϊʲô��
��1��56-2x����2��С���˵����ȷ�����ɼ�����. �������������������1����BC�ij���=Χ���ij���-AB��CD�ij���+�ŵĿ��ȣ���2�����������S��x�Ķ��κ�����ϵ��Ȼ����ݶ��κ������������Sȡ���ֵʱx��ֵ���Ӷ��ó����β���������. �����������1������AB��x�ף��ɵ�BC��54��2x��2��56��2x�� ��2����С���˵����ȷ�� �������S��x��56��2x������2��...����ͼ��ʾƽ��ֱ������ϵ�У�ÿ��С�����εı߳���Ϊ1����ABC������������ڸ���ϣ�
��1����OΪ��ת���ģ�����ABC��ʱ����ת90�㣬������ת��ġ�A1B1C1��
��2��������A1B1C1����ԭ��ԳƵġ�A2B2C2��
��3������ABC����һ��P��a��b��������������α任���P�ڡ�A2B2C2�еĶ�Ӧ��ΪP�䣬���P�������Ϊ�� ����
�ִ������������Ĺ㷺Ӧ�ã������˿����ҵ�ĸ߶ȷ�չ���ݵ��飬��ɳ��ij��С�͡���ѧ��������ҵ���Ŀ�ݹ�˾���������·������·����Ͷ�ݵĿ���ܼ����ֱ�Ϊ10�����12.1������ּٶ��ù�˾ÿ��Ͷ�ݵĿ���ܼ�������������ͬ��
��1����ÿ�ݹ�˾Ͷ���ܼ�������ƽ�������ʣ�
��2�����ƽ��ÿ��ÿ������Ͷ��0.6�������ô�ù�˾���е�21�����Ͷ��ҵ��Ա�ܷ���ɽ���6�·ݵĿ��Ͷ������
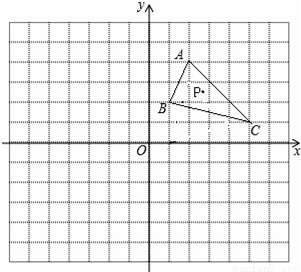
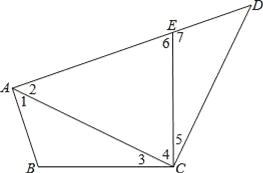
�鿴���ı���ABCD�������Σ�E��F�ֱ���DC��CB���ӳ����ϵĵ㣬��DE=BF������AE��AF��EF��
��1����֤����ADE�ա�ABF��
��2����BC=8��DE=6�����AEF�������
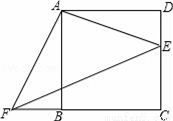
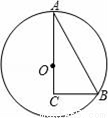
��ͼ��Բ�����Ź��Ŀ��AB=12�ף�����CD=4�ף����ŵİ뾶.
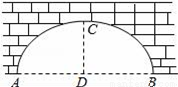
��ͼ��Rt��ABC�У���C=90�㡢��A=30�㣬��AC����ȡ��O��Բ��ʹ��O����A��B���㣬���н�����ȷ�������____________
��AO=2CO����AO=BC������OΪԲ�ģ���OCΪ�뾶��Բ��AB���У����ӳ�BC����O��D����A��B��D�ǡ�O�����ȷֵ㣮
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ͼ����������ͼ��������O��ת180��õ���ͼ���ǣ�������
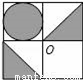
A.  B.
B.  C.
C. 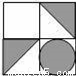 D.
D. 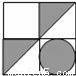
���з����ǹ���x��һԪ���η��̵��ǣ�������
A. ax2+bx+c=0 B. 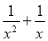 =2 C. x2+2x=x2��1 D. 3��x+1��2=2��x+1��
=2 C. x2+2x=x2��1 D. 3��x+1��2=2��x+1��
�Ķ����ϣ���m2��2mn+2n2��8n+16=0����m��n��ֵ��
��������
��m2��2mn+2n2��8n+16=0���ࣨm2��2mn+n2��+��n2��8n+16��=0
�ࣨm��n��2+��n��4��2=0���ࣨm��n��2=0����n��4��2=0����n=4��m=4��
������Ĺ۲죬̽����������⣺
��1����֪x2��2xy+2y2+6y+9=0����xy��ֵ��
��2����֪��ABC�����߳�a��b��c������������������a2+b2��10a��12b+61=0�����ABC������c��ֵ��
��3����֪a��b=8��ab+c2��16c+80=0����a+b+c��ֵ��
�鿴��ij�̼�Ԥ��һ�ֳ����ܳ����г�������12000Ԫ������һ�����ֳ��������к��Ȼ����Ӧ���̼�������26400Ԫ�����˵ڶ������ֳ��������������ǵ�һ����������2������ÿ�����۹���10Ԫ��
��1�����̼ҹ����ĵ�һ�������Ƕ��ټ���
��2����������������ÿ��150Ԫ�ļ۸����ۣ�����������ȫ�������������Ƕ���Ԫ��
�鿴����x=2m+1��y=3+4m��
��1�����ú�x�Ĵ���ʽ��ʾy��
��2�����x=4�����ʱy��ֵ��
�鿴�����һ�������������Ϊ����֮һ�������ԭ�����йص������⣬���ǰ�����Ϊԭ�����һ�����������⣮���磬ԭ�����ǡ������ε����߳��ֱ�Ϊ3��4������ε��ܳ���������ܳ�����14������һ����������������ǡ������ε��ܳ�Ϊ14����һ�߳�Ϊ3������һ�ߵij�����Ҳ�����ǡ������ε��ܳ�Ϊ14���������������ֵ�����ȵȣ�
��1����A=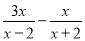 ��B=
��B=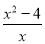 ����A��B�Ļ���
����A��B�Ļ���
��2�������1����һ�����������⣬�����������⣮
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
���Ƚ���ʽ������ѡ��һ���ʵ�����������ֵ����1��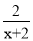 ����
����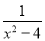 ��
��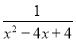 ��
��
�ⷽ��
��1��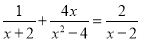 ��2��
��2��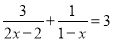
����
��1���Ȼ�������ֵ����2x��1����x+2����2x��x+1����x=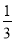 ��
��
��2����֪��a+b=4��ab=3����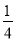 a3b+
a3b+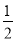 a2b2+
a2b2+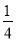 ab3��ֵ��
ab3��ֵ��
��ʽ�֡�������
��1����a+b��2+6��a+b��+9��������������������������2����x��y��2��9��x+y��2��
��3��a2��x��y��+b2��y��x���� ��4��(x2��5)2��8(5��x2)��16.
�鿴������
��1��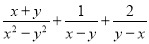 ��2��
��2��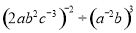
��3��a5��a7��a6��(��a3)2��2(��a3)4�� (4����x+2y��z����x��2y+z��
�鿴����֪����x�ķ�ʽ����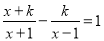 �Ľ�Ϊ��������k��ȡֵ��Χ��_________
�Ľ�Ϊ��������k��ȡֵ��Χ��_________
- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ʽ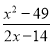 Լ�ֵĽ����_______
Լ�ֵĽ����_______
��x2+mxy+16y2����ȫƽ��ʽ����m= ________
�鿴��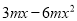 �й���ʽ��___________
�й���ʽ��___________
6����ͼ1�ij�Ϊa����Ϊb��a��b����С������ֽƬ����ͼ2��ʽ���ص��ط��ھ���ABCD�ڣ�δ�����ǵIJ��֣��������Σ�����Ӱ��ʾ�������Ͻ������½ǵ���Ӱ���ֵ�����IJ�ΪS����BC�ij��ȱ仯ʱ������ͬ���ķ��÷�ʽ��Sʼ�ձ��ֲ��䣬��a��b���㣨 ��
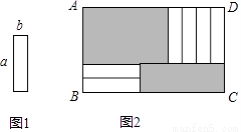
A. a=2b B. a=3b C. a=4b D. a=b
�鿴������(x2��3x��n)(x2��mx��8)�Ľ���в���x2��x3�����m��n��ֵΪ(����)
A. m��3��n��1 B. m��0��n��0 C. m����3��n����9 D. m����3��n��8
�鿴��������x�ķ�ʽ����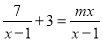 �⣬��ʵ��m��ֵ�ǣ� ��
�⣬��ʵ��m��ֵ�ǣ� ��
A. x=0��1 B. x=1��3 C. x=3��7 D. x=0��3
�鿴�� ��������- ���ͣ������
- �Ѷȣ���
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
��ʹ��ʽ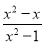 ��ֵΪ�������x��ֵ�ǣ� ��
��ֵΪ�������x��ֵ�ǣ� ��
A. x=1 B. x=0 C. x=0��x=1 D. x=0��x=��1
B �����������������������ã�x2-x=0����x2-1��0�� ��ã�x=0�� ��ѡB���ѷ�ʽ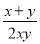 �е�x��y������3������ô��ʽ��ֵ��������
�е�x��y������3������ô��ʽ��ֵ��������
A. ����3�� B. ���� C. ��С3�� D. ��С6��
�鿴�����ʽ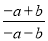 ��ȵ��ǣ� ��
��ȵ��ǣ� ��
A. 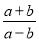 B.
B. 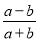 C.
C. 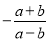 D.
D. 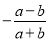
�������һ���������������г�����㣬�������Ľ����(����)
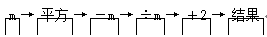
A. m B. m��2 C. m��1 D. m2+1
�鿴������������ȷ����(����)
A. m2(mn��3n��1)��m3n��3m2n B. (��3ab2)2����9a2b4
C. (��a��b)(��a��b)��b2��a2 D. 3x2y��xy��3x
�鿴������(ab2)3�Ľ������ȷ����(��)
A. a3b6 B. a3b5 C. ab6 D. ab5
�鿴�� ��������- ���ͣ���ѡ��
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
ijУ��չ����Լÿһ��ˮ�����Ϊ���˽չ���һ����������Լ��ˮ�IJ������Ӱ��꼶��400��ͬѧ��ѡ��20��ͬѧͳ���˽���Լ�ͥһ���µĽ�ˮ��������±���
��ˮ��m3�� | 0.2 | 0.25 | 0.3 | 0.4 | 0.5 |
��ͥ�������� | 2 | 4 | 6 | 7 | 1 |
�ֱ������20����ͥ��ˮ����λ�������������������400��ͬѧ�ļ�ͥһ���½�Լ��ˮ��������Լ�Ƕ���m3��
130 ������������������ȸ�����λ���������Ķ�������������ݵ���λ�����������ټ������20��ͬѧ���Լ�ͥһ���µĽ�ˮ����ƽ������������ƽ������Ȼ���������400���ɽ�� �����������20����ͥ��ˮ����λ���ǵ�10�����͵�11������ƽ������0.3��������0.4�� 20��ͬѧ���Լ�ͥһ����ƽ����Լ��ˮ�ǣ� ��0.2��2+0.25��4+0.3��6+0.4��7+0.5��1����2...��ͼ����ABC�͡�ABD�У���C=��D=Rt�ϣ�E��BC���ϵ����ߣ�����˵��CE=DE�����ɣ�
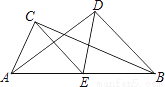
��ͼ���ı���ABCD�У�E����AD�ϣ����С�BAE=��BCE=��ACD=90�㣬��BC=CE����֤����ABC���DECȫ�ȣ�
�������x�IJ���ʽk��x+6��0����������Ϊ1��2��3����ôk��ȡֵ��Χ�Ƕ��٣�
�鿴���ⲻ��ʽ�飺  ,���ѽ⼯�������ϱ�ʾ������
,���ѽ⼯�������ϱ�ʾ������
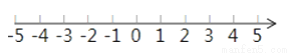
��M��a����5�����N����2��b������x��Գƣ���a+b=________��
�鿴�� ��������- ���ͣ������
- �Ѷȣ��е�
 Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������
Copyright @ 2008-2013 ����5 ѧϰ�� ManFen5.COM. All Rights Reserved.������

