题目内容
19.设圆内接正三角形面积是S1,圆内接正方形面积是S2,圆内接正六边形面积是S3,当它们的边心距相等时,S1、S2、S3之间的数量关系是( )| A. | S1>S2>S3 | B. | S2>S1>S3 | C. | S3>S1>S2 | D. | S3>S2>S1 |
分析 设正三角形、正方形、正六边形的边心距为r;在正三角形ABC中,作OM⊥AB于M,求出正三角形的面积S1;在正方形中,作OM⊥AB于M,求出正方形的面积S2;在正六边形中,作OM⊥AB于M,求出正六边形的面积S3,即可得出结果.
解答 解:设正三角形、正方形、正六边形的边心距为r;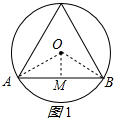
在正三角形ABC中,作OM⊥AB于M,连接OA、OB;如图1所示:
则OM=r,OA=2r,
∴AM=$\sqrt{3}$r,
∴AB=2$\sqrt{3}$r,
∴正三角形的面积S1=3×$\frac{1}{2}$×2$\sqrt{3}$r×r=3$\sqrt{3}$r${\;}^{{\;}^{2}}$;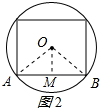
在正方形中,作OM⊥AB于M,连接OA、OB,如图2所示:
则OM=r,
∴AB=2r,
∴正方形的面积S2=(2r)2=4r2;
在正六边形中,作OM⊥AB于M,连接OA、OB,如图3所示: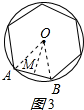
则OM=r,AM=$\frac{\sqrt{3}}{3}$r,
∴AB=$\frac{2\sqrt{3}}{3}$r,
∴正六边形面积是S3=6×$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$r×r=2$\sqrt{3}$r2,
∵3$\sqrt{3}$>4>2$\sqrt{3}$,
∴S1>S2>S3,
故选:A.
点评 本题考查了正多边形和圆,正三角形、正方形、正六边形的性质以及面积的计算方法;把正三角形、正方形、正六边形的面积分别用相等的边心距表示出来是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
4.一个圆柱体的半径比原来圆柱体的半径多3倍,高是原来的$\frac{1}{4}$,这个圆柱体体积是原来圆柱体体积的( )
| A. | $\frac{3}{4}$倍 | B. | 1倍 | C. | 2倍 | D. | 4倍 |
11.下列方程中,是一元一次方程的是( )
| A. | 3x-2y+z=0 | B. | $\frac{x}{7}$=-1 | C. | $\frac{2}{1-x}$=3 | D. | x2-x=1 |
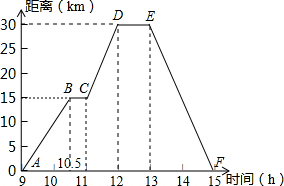 小强骑自行车去郊游,右图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小明9点离开家,15点回家.根据这个图象,请你回答下列问题:
小强骑自行车去郊游,右图表示他离家的距离y(千米)与所用的时间x(小时)之间关系的函数图象,小明9点离开家,15点回家.根据这个图象,请你回答下列问题: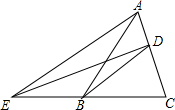 如图.△ABC的面积为6,D为AC边上一点,AD=$\frac{1}{2}$CD,连接BD.过点A作DB的平行线交CB的延长线于点E,连接DE,求△EDB的面积.
如图.△ABC的面积为6,D为AC边上一点,AD=$\frac{1}{2}$CD,连接BD.过点A作DB的平行线交CB的延长线于点E,连接DE,求△EDB的面积.