题目内容
7．解方程：（1）（x-1）（x-4）=10
（2）$\frac{{x}^{2}-1}{3}$+$\frac{x}{2}$=x．
分析 （1）方程整理后，利用因式分解法求出解即可；
（2）方程整理后，利用因式分解法求出解即可．
解答 解：（1）方程整理得：x2-5x-6=0，
分解因式得：（x-6）（x+1）=0，
解得：x1=6，x2=-1；
（2）去分母得：2x2-2+3x=6x，即2x2-3x-2=0，
分解因式得：（2x+1）（x-2）=0，
解得：x1=-$\frac{1}{2}$，x2=2．
点评 此题考查了解一元二次方程-因式分解法，熟练掌握因式分解法是解本题的关键．
练习册系列答案
相关题目
17．方程5x-1=4x2的两根之和为（ ）
| A． | $\frac{5}{4}$ | B． | -$\frac{5}{4}$ | C． | $\frac{1}{4}$ | D． | -$\frac{1}{4}$ |
15．
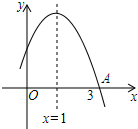如图所示是二次函数y=ax2+bx+c图象的一部分，图象过A点（3，0），二次函数图象对称轴为直线x=1，给出五个结论：①bc＞0；②a+b+c＜0；③4a-2b+c＞0；④方程ax2+bx+c=0的根为x1=-1，x2=3；⑤当x＜1时，y随着x的增大而增大．其中正确结论是（ ）
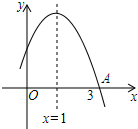如图所示是二次函数y=ax2+bx+c图象的一部分，图象过A点（3，0），二次函数图象对称轴为直线x=1，给出五个结论：①bc＞0；②a+b+c＜0；③4a-2b+c＞0；④方程ax2+bx+c=0的根为x1=-1，x2=3；⑤当x＜1时，y随着x的增大而增大．其中正确结论是（ ）| A． | ①②③ | B． | ①③④ | C． | ②③④ | D． | ①④⑤ |
如图，将长方形ABCD边AD沿折痕AE折叠，使点D落在BC上的点F处，已知AB=6，△ABF的面积是24，求DE的长．
17．
如图是一个数值转换机，若输入的x的值为7，则输出的结果是（ ）
如图是一个数值转换机，若输入的x的值为7，则输出的结果是（ ）| A． | 12 | B． | -15 | C． | 27 | D． | 21 |