题目内容
2. 如图,将长方形ABCD边AD沿折痕AE折叠,使点D落在BC上的点F处,已知AB=6,△ABF的面积是24,求DE的长.
如图,将长方形ABCD边AD沿折痕AE折叠,使点D落在BC上的点F处,已知AB=6,△ABF的面积是24,求DE的长.
分析 先根据三角形的面积公式求得BF的长,然后根据勾股定理可求得AF=10,由翻折的性质和矩形的性质可知BC=10,故此FC=2,最后在△EFC中,由勾股定理列方程求解即可.
解答 解:∵SABF=24,
∴$\frac{1}{2}AB•BF=24$,即$\frac{1}{2}×6×BF=24$.
解得:BF=8.
在Rt△ABF中由勾股定理得:AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10.
由翻折的性质可知:BC=AD=AF=10,ED=FE.
∴FC=10-8=2.
设DE=x,则EC=6-x.
在Rt△EFC中,由勾股定理得:EF2=FC2+EC2,x2=4+(6-x)2.
解得:x=$\frac{10}{3}$.
∴ED=$\frac{10}{3}$.
点评 本题主要考查的是翻折的性质、三角形的面积公式、勾股定理的应用,根据勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
13.方程x2-2x-1=0的两实根为x1、x2,则x1•x2的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
14.地球到月球的平均距离是384400千米,把384400这个数用科学记数法表示为( )
| A. | 3844×102 | B. | 0.3844×104 | C. | 3.844×108 | D. | 3.844×105 |
11.2013年绍兴市生产总值是3967.29亿元,其中3967.29亿元用科学记数法表示是( )
| A. | 3967.29×103元 | B. | 3.96729×1011元 | C. | 0.396729×1011元 | D. | 3.96729×108元 |
12.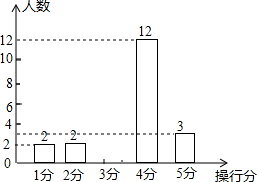 某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:
某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:
(1)补全统计表和条形统形图;
(2)若要在操行得分为5分的5名同学中选出两名同学作“本周明星”,用画树状图或列表的方法求出选为“本周明星”的正好是一名男同学和一名女同学的概率.
 某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:
某班有50名同学,男、女生人数各占一半,在本周操行评定中操行得分情况如图统计表中所示,图10是该班本周男生操行得分的条形统计图:| 操行分得分 | 1分 | 2分 | 3分 | 4分 | 5分 |
| 人数 | 2 | 4 | 9 | 30 | 5 |
(2)若要在操行得分为5分的5名同学中选出两名同学作“本周明星”,用画树状图或列表的方法求出选为“本周明星”的正好是一名男同学和一名女同学的概率.
 如图:
如图: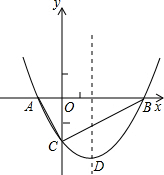 如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).
如图,抛物线y=$\frac{1}{2}$x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).