题目内容
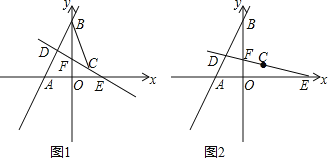
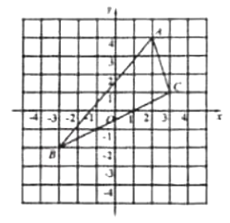
【题目】如图,已知抛物线 y![]() x2 bxc经过△ ABC 的三个顶点,其中点 A(0,1),点 B(9,10),AC∥x 轴,点 P 是直线 AC 下方抛物线上的动点,过点 P 且与 y 轴平行的直线 l 与直线 AB、AC 分别交于点 E、F.
x2 bxc经过△ ABC 的三个顶点,其中点 A(0,1),点 B(9,10),AC∥x 轴,点 P 是直线 AC 下方抛物线上的动点,过点 P 且与 y 轴平行的直线 l 与直线 AB、AC 分别交于点 E、F.
(1)求抛物线的函数表达式;
(2)如图 1,当四边形 AECP 的面积最大时,求点 P 的坐标和四边形 AECP 的最大面积;
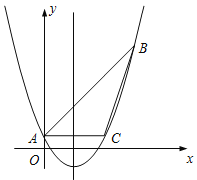
(3)如图 2,当点 P 为抛物线的顶点时,在直线 AC 上是否存在点 Q,使得以 C,P,Q 为顶点的三角形与△ ABC 相似?若存在,请直接写出点 Q 的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 时,四边形
时,四边形![]() 的面积最大值是
的面积最大值是![]() ,此时
,此时![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据平行于x轴的直线上点的纵坐标相等,可得C点的纵坐标,根据自变量与函数值的对应关系,可得C点坐标,根据待定系数法,可得AB的解析式,根据直线上的点满足函数解析式,可得E点坐标,根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PE的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案;
(3)根据等腰直角三角形的性质,可得∠PCF=∠EAF,根据相似三角形的判定,可得关于t的方程,根据解方程,可得答案.
(1)将A(0,1),B(9,10)代入函数解析式,
得 ,解得
,解得![]() ,
,
抛物线的解析式y=![]() x2-2x+1;
x2-2x+1;
(2)∵![]() 轴,
轴,![]() ,
,
∴![]() ,
,
解得![]() ,
,![]() (舍),
(舍),
即![]() 点坐标为
点坐标为![]() ,
,
∵点![]() ,点
,点![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
设![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴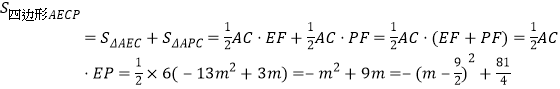 ,
,
∵![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 的面积最大值是
的面积最大值是![]() ,此时
,此时![]() ;
;
(3)∵![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理可得![]() ,
,
∴![]() ,
,
∴在直线![]() 上存在满足条件得点
上存在满足条件得点![]() ,设
,设![]() 且
且![]() ,
,![]() ,
,![]() ,
,
∵以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,
①当![]() 时,
时,![]() ,
,![]() ,解得
,解得![]() ,
,![]() ;
;
②当![]() 时,∴
时,∴![]() ,
,![]() ,解得
,解得![]() ,
,![]() .
.
综上所述:当点![]() 为抛物线的顶点时,在直线
为抛物线的顶点时,在直线![]() 上存在点
上存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,
相似,![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.

 名校课堂系列答案
名校课堂系列答案