题目内容
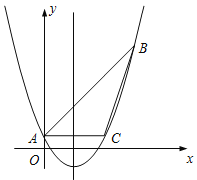
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+6与x轴、y轴分别交于A、B两点,且OB=![]() OA,直线l2:y=k2x+b经过点C(
OA,直线l2:y=k2x+b经过点C(![]() ,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
,1),与x轴、y轴、直线AB分别交于点E、F、D三点.
(1)求直线l1的解析式;
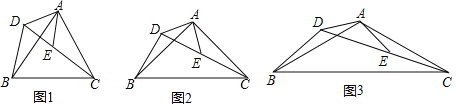
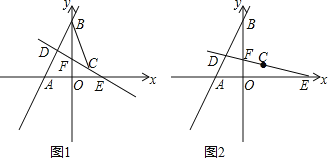
(2)如图1,连接CB,当CD⊥AB时,求点D的坐标和△BCD的面积;
(3)如图2,当点D在直线AB上运动时,在坐标轴上是否存在点Q,使△QCD是以CD为底边的等腰直角三角形?若存在,请直接写出点Q的坐标,若不存在,请说明理由.
【答案】(1)y=![]() x+6;(2)D(﹣
x+6;(2)D(﹣![]() ,3),S△BCD=4
,3),S△BCD=4![]() ;(3)存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2
;(3)存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2![]() )或(6﹣4
)或(6﹣4![]() ,0)或(﹣4
,0)或(﹣4![]() ﹣6,0)
﹣6,0)
【解析】
(1)根据待定系数法可得直线l1的解析式;
(2)如图1,过C作CH⊥x轴于H,求点E的坐标,利用C和E两点的坐标求直线l2的解析式,与直线l1列方程组可得点D的坐标,利用面积和可得△BCD的面积;
(3)分四种情况:在x轴和y轴上,证明△DMQ≌△QNC(AAS),得DM=QN,QM=CN,设D(m,![]() m+6)(m<0),表示点Q的坐标,根据OQ的长列方程可得m的值,从而得到结论.
m+6)(m<0),表示点Q的坐标,根据OQ的长列方程可得m的值,从而得到结论.
解:(1)y=k1x+6,
当x=0时,y=6,
∴OB=6,
∵OB=![]() OA,
OA,
∴OA=2![]() ,
,
∴A(﹣2![]() ,0),
,0),
把A(﹣2![]() ,0)代入:y=k1x+6中得:﹣2
,0)代入:y=k1x+6中得:﹣2![]() k1+6=0,
k1+6=0,
k1=![]() ,
,
∴直线l1的解析式为:y=![]() x+6;
x+6;
(2)如图1,过C作CH⊥x轴于H,
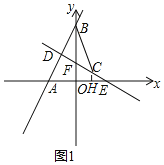
∵C(![]() ,1),
,1),
∴OH=![]() ,CH=1,
,CH=1,
Rt△ABO中,![]() ,
,
∴AB=2OA,
∴∠OBA=30°,∠OAB=60°,
∵CD⊥AB,
∴∠ADE=90°,
∴∠AED=30°,
∴EH=![]() ,
,
∴OE=OH+EH=2![]() ,
,
∴E(2![]() ,0),
,0),
把E(2![]() ,0)和C(
,0)和C(![]() ,1)代入y=k2x+b中得:
,1)代入y=k2x+b中得: ,
,
解得: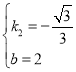 ,
,
∴直线l2:y=![]() x+2,
x+2,
∴F(0,2)即BF=6﹣2=4,
则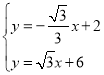 ,解得
,解得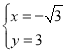 ,
,
∴D(﹣![]() ,3),
,3),
∴S△BCD=![]() BF(xC﹣xD)=
BF(xC﹣xD)=![]() ;
;
(3)分四种情况:
①当Q在y轴的正半轴上时,如图2,过D作DM⊥y轴于M,过C作CN⊥y轴于N,
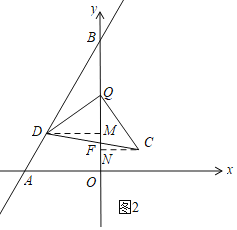
∵△QCD是以CD为底边的等腰直角三角形,
∴∠CQD=90°,CQ=DQ,
∴∠DMQ=∠CNQ=90°,
∴∠MDQ=∠CQN,
∴△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=![]() ,
,
设D(m,![]() m+6)(m<0),则Q(0,﹣m+1),
m+6)(m<0),则Q(0,﹣m+1),
∴OQ=QN+ON=OM+QM,
即﹣m+1=![]() m+6+
m+6+![]() ,
,
![]() ,
,
∴Q(0,2![]() );
);
②当Q在x轴的负半轴上时,如图3,过D作DM⊥x轴于M,过C作CN⊥x轴于N,
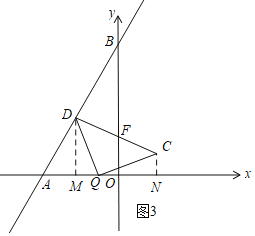
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=1,
设D(m,![]() m+6)(m<0),则Q(m+1,0),
m+6)(m<0),则Q(m+1,0),
∴OQ=QN﹣ON=OM﹣QM,
即![]() m+6-
m+6-![]() =﹣m﹣1,
=﹣m﹣1,
m=5﹣4![]() ,
,
∴Q(6﹣4![]() ,0);
,0);
③当Q在x轴的负半轴上时,如图4,过D作DM⊥x轴于M,过C作CN⊥x轴于N,
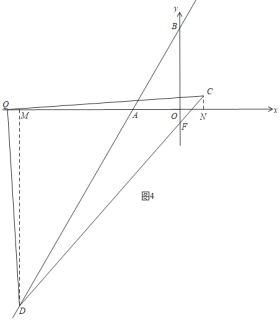
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=1,
设D(m,![]() m+6)(m<0),则Q(m﹣1,0),
m+6)(m<0),则Q(m﹣1,0),
∴OQ=QN﹣ON=OM+QM,
即﹣![]() m﹣6﹣
m﹣6﹣![]() =﹣m+1,
=﹣m+1,
m=﹣4![]() ﹣5,
﹣5,
∴Q(﹣4![]() ﹣6,0);
﹣6,0);
④当Q在y轴的负半轴上时,如图5,过D作DM⊥y轴于M,过C作CN⊥y轴于N,
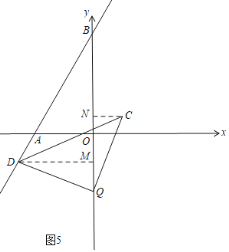
同理得:△DMQ≌△QNC(AAS),
∴DM=QN,QM=CN=![]() ,
,
设D(m,![]() m+6)(m<0),则Q(0,m+1),
m+6)(m<0),则Q(0,m+1),
∴OQ=QN﹣ON=OM+QM,
即﹣![]() m﹣6+
m﹣6+![]() =﹣m﹣1,
=﹣m﹣1,
m=﹣2![]() ﹣1,
﹣1,
∴Q(0,﹣2![]() );
);
综上,存在点Q,使△QCD是以CD为底边的等腰直角三角形,点Q的坐标是(0,±2![]() )或(6﹣4
)或(6﹣4![]() ,0)或(﹣4
,0)或(﹣4![]() ﹣6,0).
﹣6,0).

 阅读快车系列答案
阅读快车系列答案