题目内容
6.若2m+2n=3,2m•2n=1,则4m+4n=7.分析 根据已知条件和完全平方公式的变形公式得到4m+4n=(2m+2n)2-2•2m•2n.
解答 解:∵2m+2n=3,2m•2n=1,
∴4m+4n
=(2m+2n)2-2•2m•2n
=32-2×1
=7.
故答案是:7.
点评 本题主要考查完全平方公式,熟记公式的几个变形公式对解题大有帮助.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
5.下列选项中,与a3b是同类项的是( )
| A. | -ab | B. | -ab3 | C. | a3b3 | D. | $\frac{1}{2}$a3b |
9.要使分式$\frac{1}{3-x}$有意义,则( )
| A. | x≠3 | B. | x=3 | C. | x>3 | D. | x>-3 |
10.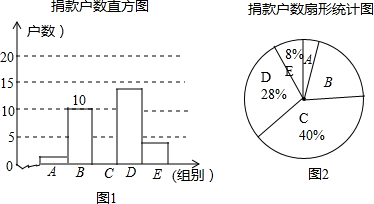 我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题
我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题
(1)A组捐款户数是多少?本次调查的样本容量是多少?
(2)求出C组的频数并补全直方图;
(3)若该社区有500户住户,请估计捐款不少于300元的户数是多少?
 我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题
我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题(1)A组捐款户数是多少?本次调查的样本容量是多少?
(2)求出C组的频数并补全直方图;
(3)若该社区有500户住户,请估计捐款不少于300元的户数是多少?
| 组别 | 捐款额(x)元 |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x≥400 |