题目内容
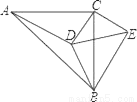
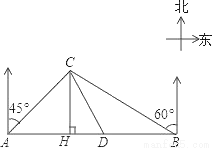
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A、B两地,分别有甲、乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C,过点C作CH⊥AB于H.
(1)求牧民区C到B地的距离(结果用根式表示);
(2)一天,乙医疗队的医生要到牧民区C出诊,她先由B地搭车沿公路AB到D处(BD<AB)转车,再由D地沿DC方向到牧民区C.若C、D两地距离是B、C两地距离的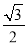 倍,求B、D两地的距离.(结果精确到0.1千米 参考数据:
倍,求B、D两地的距离.(结果精确到0.1千米 参考数据: 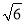 ≈2.449,
≈2.449, 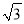 ≈1.732,
≈1.732, 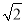 ≈1.414)
≈1.414)
练习册系列答案
相关题目



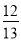 , 则tanA的值为( )
, 则tanA的值为( )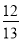 B.
B. 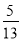 C.
C. 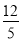 D.
D. 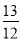
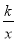 经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为6,则k的值是_____.
经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为6,则k的值是_____.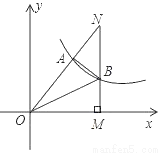
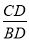 =1.其中正确的是( )
=1.其中正确的是( )