Question

如图，已知AB是⊙O的直径，BC是⊙O的弦，弦ED⊥AB于点F，交BC于点G，过点C的直线与ED的延长线交于点P，PC=PG．

（1）求证：PC是⊙O的切线；

（2）当点C在劣弧AD上运动时，其他条件不变，若BG²=BF•BO．求证：点G是BC的中点；

（3）在满足（2）的条件下，AB=10，ED=4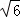，求BG的长．

Answer 1

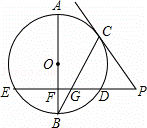
（1）证明：连OC，如图，

∵ED⊥AB，

∴∠FBG+∠FGB=90°，

又∵PC=PG，

∴∠1=∠2，

而∠2=∠FGB，∠4=∠FBG，

∴∠1+∠4=90°，即OC⊥PC，

∴PC是⊙O的切线；

（2）证明：连OG，如图，

∵BG²=BF•BO，即BG：BO=BF：BG，

而∠FBG=∠GBO，

∴△BGO∽△BFG，

∴∠OGB=∠BFG=90°，

即OG⊥BG，

∴BG=CG，即点G是BC的中点；

（3）解：连OE，如图，

∵ED⊥AB，

∴FE=FD，

而AB=10，ED=4，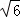

∴EF=2，OE=5，

在Rt△OEF中，OF===1，

∴BF=5﹣1=4，

∵BG²=BF•BO，

∴BG²=BF•BO=4×5，

∴BG=2．