题目内容
已知直线y=kx+b经过点A(0,-2),且与坐标轴围成的直角三角形的面积为4,求k值.
考点:待定系数法求一次函数解析式
专题:
分析:先求得b=-2;再令y=0求出x的值即可得出直线与坐标轴的交点,再根据三角形的面积公式即可得出结论.
解答:解:∵直线y=kx+b经过点A(0,-2),
∴b═-2,
令y=0,则x=
,
∴直线与坐标轴的交点分别为(0,-2),(
,0),
∴S=
×|
|×2=4,解得k=±
.
∴b═-2,
令y=0,则x=
| 2 |
| k |
∴直线与坐标轴的交点分别为(0,-2),(
| 2 |
| k |
∴S=
| 1 |
| 2 |
| 2 |
| k |
| 1 |
| 2 |
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
代数式6x2y+
,4xy+y2,
x+y,
,-2,a中,不是整式的有( )
| 1 |
| x |
| 1 |
| 3 |
| 2 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列图案中,不是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
 在平行四边形ABCD中,点E为AD的中点,连接CE,点M、N为CE上两点,且BM∥DN.连接DM并延长交AB于F,若BF=2AF,求
在平行四边形ABCD中,点E为AD的中点,连接CE,点M、N为CE上两点,且BM∥DN.连接DM并延长交AB于F,若BF=2AF,求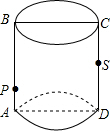 如图所示,圆柱的轴截面ABCD是边长为4的正方形,动点P的初始位置在AB上,AP=1,点P由此出发,沿着圆柱的侧面移动到CD的中点S,点P与点S之间的最短距离是
如图所示,圆柱的轴截面ABCD是边长为4的正方形,动点P的初始位置在AB上,AP=1,点P由此出发,沿着圆柱的侧面移动到CD的中点S,点P与点S之间的最短距离是