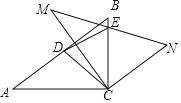
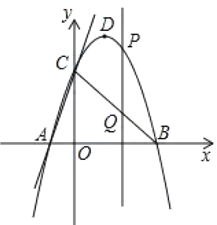
题目内容
【题目】如图,在平面直角坐标系中,抛物线![]() 与直线
与直线![]() 交于点
交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且点
,且点![]() 在
在![]() 轴上,
轴上,![]() 为抛物线
为抛物线![]() 的顶点.
的顶点.
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)若![]() 是第一象限内抛物线上的一个运动的点,点
是第一象限内抛物线上的一个运动的点,点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,求当
,求当![]() 为何值时,线段
为何值时,线段![]() 的长最大?最大值是多少?并直接写出此时点
的长最大?最大值是多少?并直接写出此时点![]() 的坐标;
的坐标;
(3)在(2)的条件下,当![]() 的长取得最大值时,在坐标平面内是否存在点
的长取得最大值时,在坐标平面内是否存在点![]() ,使以
,使以![]() 为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点
为顶点的四边形是平行四边形?若存在,请直接写出符合条件的点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
【答案】(1)![]() ;点
;点![]() 的坐标为
的坐标为![]() ;(2)当
;(2)当![]() 时,
时,![]() 的长最大,最大值是
的长最大,最大值是![]() ,
,![]() ;(3)存在,
;(3)存在,![]() ,
,![]() ,
,![]()
【解析】
(1)根据直线方程得出A,C两点的坐标,再代入抛物线,即可求出解析式,再对解析式进行配方即可得出D点的坐标;
(2)用m表示出PQ的坐标,根据题意列出关于m的函数解析式,求解即可;
(3)需要分类讨论:①以PQ为边时,②以PQ为对角线时.
解:(1)由直线![]() 可知
可知![]() ,
,![]() ,
,
把点![]() 和点
和点![]() 代入
代入![]() 中,得
中,得![]()
解得:![]() ,
,
![]() ,
,
又∵![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
(2)将y=0代入抛物线![]() ,
,
得B点坐标为(3,0),
∵有(1)得C点的坐标为![]() ,
,
∴可知![]() 的解析式是
的解析式是![]() ,
,
∴设![]() ,
,![]()
![]()
当![]() 时,
时,![]() 的长最大,最大值是
的长最大,最大值是![]() ,
,
![]() ;
;
(3)存在,在(2)的条件下P点的坐标为![]() ,Q点的坐标为
,Q点的坐标为![]() ,
,
①以PQ为边时,则AH∥PQ,即H点与A点的横坐标一致时,能让以![]() 为顶点的四边形是平行四边形,此时根据设H点的坐标为(-1,a),
为顶点的四边形是平行四边形,此时根据设H点的坐标为(-1,a),
根据平行四边形的性质可得│AH│=│PQ│,即│a│-0=![]() ,
,
解得a=±![]() ,
,
∴此时H的坐标有两种情况:![]() ,
,![]() ,
,
②以PQ为对角线时,则有AQ∥PH,能让以![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
此时设H点的坐标为(a,b),
根据图象和平行四边形的性质可得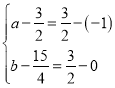 ,
,
解得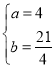 ,
,
∴此时H的坐标为:![]() ,
,
综上符合题意的H点的坐标有:![]() ,
,![]() ,
,![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
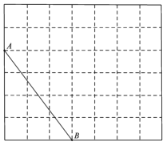
同步拓展阅读系列答案【题目】参照学习函数的过程与方法,探究函数y=![]() 的图象与性质.
的图象与性质.
因为y=![]() ,即y=﹣
,即y=﹣![]() +1,所以我们对比函数y=﹣
+1,所以我们对比函数y=﹣![]() 来探究.
来探究.
列表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y=![]() 相应的函数值为纵坐标,描出相应的点,如图所示:
相应的函数值为纵坐标,描出相应的点,如图所示:
(1)请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当x<0时,y随x的增大而 ;(填“增大”或“减小”)
②y=![]() 的图象是由y=﹣
的图象是由y=﹣![]() 的图象向 平移 个单位而得到;
的图象向 平移 个单位而得到;
③图象关于点 中心对称.(填点的坐标)
(3)设A(x1,y1),B(x2,y2)是函数y=![]() 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
的图象上的两点,且x1+x2=0,试求y1+y2+3的值.
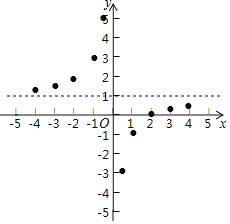
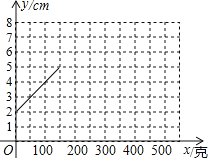
【题目】弹簧是一种利用弹性来工作的机械零件,用弹性材料制成的零件在外力作用下发生形变,除去外力后又恢复原状.某班同学在探究弹簧的长度与所受外力的变化关系时,通过实验记录得到的数据如下表:
砝码的质量x(克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
指针的位置y(cm) | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究,下面是小腾的探究过程,请补充完整.
(1)根据上述表格在平面直角坐标系中补全该函数的图象;
(2)根据画出的函数图象,写出:
①当x=0时,y= ,它的实际意义是 ;
②当指针的位置y不变时,砝码的质量x的取值范围为 .