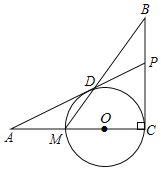
题目内容
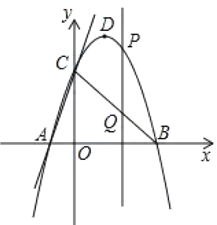
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 的左侧,抛物线与
的左侧,抛物线与![]() 轴正半轴交于点
轴正半轴交于点![]() ,分别连接
,分别连接![]() 、
、![]() ,则有
,则有![]() ,
,![]() ,
,
(1)求抛物线的函数表达式;
(2)设![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 为线段
为线段![]() 上任意一点,过点
上任意一点,过点![]() 作
作![]() 轴的垂线分别交直线
轴的垂线分别交直线![]() 及抛物线于点
及抛物线于点![]() 、点
、点![]() ,当
,当![]() 是锐角三角形时,求
是锐角三角形时,求![]() 的取值范围.
的取值范围.
(3)在(2)的前提下,设![]() ,求
,求 ![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由![]() ,在
,在![]() 中,
中,![]() ,得
,得![]() ,
,![]() ,根据
,根据![]() ,得到
,得到![]() ,进而得到
,进而得到![]() ,在
,在![]() 中
中![]() ,
,![]() ,得到
,得到![]() ,再根据又
,再根据又![]() ,
,![]() ,得到
,得到![]() ,
,![]() ,再根据对称轴为直线
,再根据对称轴为直线![]() ,得到
,得到![]() ,
,![]() ,
,![]() 且过点
且过点![]() ,即可求解.
,即可求解.
(2)由![]() 为锐角三角形,考虑:
为锐角三角形,考虑:![]() 时:
时:![]() ,
,![]() ,
, ,得到
,得到![]() ;
; ![]() 时:
时: ,得到
,得到![]() ,即可求解.
,即可求解.
(3)令![]() ,得到
,得到![]() ,进而得到
,进而得到![]() ,继续得到
,继续得到![]() ,即可求解.
,即可求解.
解:(1)由![]()
在![]() 中,
中,![]()
得![]()
![]()
∵![]() ,∴
,∴![]()
∴![]() .
.
在此![]() 中
中![]()
![]()
∴![]() .
.
又∵![]() ,
,![]()
∴![]() .
.
∴![]() ,
,![]()
∴![]() ,
,![]()
又对称轴为直线![]()
∴![]()
∴![]() ,
,![]()
∴![]() 且过点
且过点![]()
∴![]()
(2)由![]() 为锐角三角形
为锐角三角形
考虑:![]() 时
时
![]() 时,
时,
ⅰ)若![]() ,
,![]() ,
,![]()

![]()
ⅱ)若![]()

![]()
∴![]()
(3)令![]()
∴![]()
解得:![]()
∴![]()
∴![]()
![]()
∴![]()
![]()
![]()
![]()
∴![]() 的最大值为
的最大值为![]()




练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
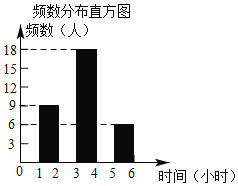
【题目】某中学兴趣小组为了解全校学生星期六和星期日在家使用手机的情况,兴趣小组随机抽取若干名学生,调查他们周末两天的使用手机时间,并根据调查结果绘制了下面两幅不完整的统计表和统计图.根据图表信息,解答下列问题:
阅读时间 (小时) | 频数 (人) | 频率 |
1≤x<2 | 9 | 0.15 |
2≤x<3 | a | m |
3≤x<4 | 18 | 0.3 |
4≤x<5 | 12 | n |
5≤x<6 | 6 | 0.1 |
合计 | b | 1 |
(1)填空:a= ,b= ,m= ,n= :
(2)将频数分布直方图补充完整;
(3)这个中学的学生共有1200人,根据上面信息来估算全校学生中周末两天使用手机时间不低于4小时的学生大约有多少人?