题目内容
17.先化简分式$\frac{2x}{{x}^{2}-1}$•$\frac{x+1}{x}$,然后请你选取一个合适的x的值,使分式的值为一个正数.分析 先把分母因式分解,再约分得到原式=$\frac{2}{x-1}$,然后把x=9代入计算即可.
解答 解:原式=$\frac{2x}{(x+1)(x-1)}$•$\frac{x+1}{x}$
=$\frac{2}{x-1}$,
当x=9时,原式=$\frac{2}{9-1}$=$\frac{1}{4}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
12.若正n边形的每个内角都等于150°,则n=( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
6.下列命题的逆命题正确的是( )
| A. | 直角都相等 | B. | 对顶角相等 | ||
| C. | 锐角三角形的高都在三角形内 | D. | 内错角相等 |
 如图,若AB∥CD,EF∥BO,MN∥PD,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
如图,若AB∥CD,EF∥BO,MN∥PD,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.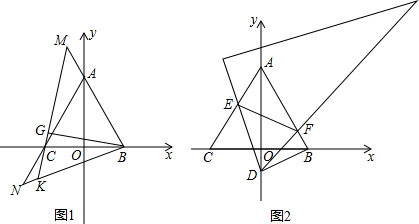
 如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.