Question

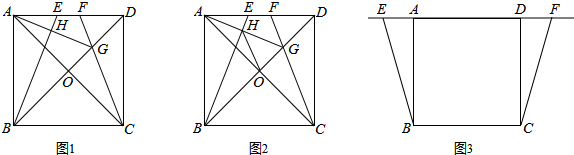
如图1，△ABC中，AB=AC，过B点作射线BE，过C点作射线CF，使∠ABE=∠ACF，且射线BE，CF交于点D．过A点作AM⊥BD于M．
（1）求证：BM=DM+DC．
（2）如图2，将射线BE，CF分别绕点B和点C顺时针旋转至如图位置，若∠ABE=∠ACF仍然成立，射线BE交射线CF的反向延长线于点D，过A点作AM⊥BD于M．请问（1）中的结论是否还成立？如果成立，请证明．如果不成立，线段BM，DM，DC又有怎样的数量关系？并证明你的结论．

Answer 1

考点：全等三角形的判定与性质,等腰三角形的性质

专题：

分析：（1）作AN⊥CF于N，连接AD，先通过△AMB≌△ANC求得BM=CN=CD+DN，AM=AN，然后通过证明RT△AMD≌RT△AND得出DM=DN，即可求得．
（2）作AN⊥CF于N，连接AD，先通过△AMB≌△ANC求得BM=CN=DN-DC，AM=AN，然后通过证明RT△AMD≌RT△AND得出DM=DN，即可求得BM=DM-DC．

解答：解：（1）作AN⊥CF于N，连接AD，
∵AM⊥BD，
∴∠AMB=∠ADC=90°，
在△AMB与△ANC中，

∠ABE=∠ACF ∠AMB=∠ADC AB=AC

∴△AMB≌△ANC（AAS）
∴BM=CN=CD+DN，AM=AN，
在Rt△AMD与RT△AND中

AM=AN AD=AD

∴RT△AMD≌RT△AND（HL）
∴DM=DN，
∴BM=CD+DM．

（2）不成立，BM=DM-DC；
作AN⊥CF于N，连接AD，
∵AM⊥BD，
∴∠AMB=∠ADC=90°，
在△AMB与△ANC中，

∠ABE=∠ACF ∠AMB=∠ADC AB=AC

∴△AMB≌△ANC（AAS）
∴BM=CN=DN-DC，AM=AN，
在Rt△AMD与RT△AND中

AM=AN AD=AD

∴RT△AMD≌RT△AND（HL）
∴DM=DN，
∴BM=DM-DC．

点评：本题考查了全等三角形的判定和性质，直角三角形全等的判定和性质，增添辅助线构建全等三角形是本题的关键．