Question

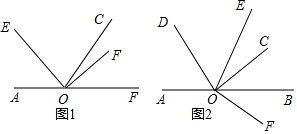
11．已知O为直线AB上的一点，∠EOF为直角，OC平分∠BOE．
（1）如图1，若∠AOE=45°，则∠COF=22.5度．
（2）如图1，若∠AOE=n°（0＜n＜90），求∠COF的度数；（用含n的式子表示）．
（3）如图2，若若∠AOE=n°（90＜n＜180），OD平分∠AOC，且∠AOD-∠BOF=45°，求n的值．

Answer 1

分析 （1）由∠AOE=45°，可以求得∠BOE=135°，再由OC平分∠BOE，可求得∠COE=67.5°，∠EOF为直角，所以可得∠COF=∠EOF-∠EOC=22.5°；
（2）由（1）的方法即可得到∠COF=$\frac{1}{2}$n°；
（3）先设∠BOF为x°，再根据角的关系得出方程，解答后求出n的值即可．

解答 解：（1）∵∠AOE=45°，
∴∠BOE=135°，
∵OC平分∠BOE，
∴∠COE=67.5°，
∵∠EOF为直角，
∴∠COF=∠EOF-∠EOC=22.5°，
故答案为：22.5；
（2））∵∠AOE=n°，
∴∠BOE=180°-n°，
∵OC平分∠BOE，
∴∠COE=$\frac{1}{2}$（180°-n°），
∵∠EOF为直角，
∴∠COF=∠EOF-∠EOC=90°-$\frac{1}{2}$（180°-n°）=$\frac{1}{2}$n°，
故答案为：$\frac{1}{2}$n°；
（3）设∠BOF为x°，∠AOD为（x+45）°，∠EOB为（90-x）°，OC平分∠BOE，
则可得：∠AOD+∠DOC+∠EOB=∠AOB+∠EOC．
x+45+x+45+90-x=180+$\frac{1}{2}$×（90-x），
解得：x=30，
所以可得：∠EOB=（90-x）°=60°，
∠AOE=180°-∠EOB=180°-60°=120°，
故n的值是120．

点评 本题考查了角平分线定义，邻补角定义，角的和差，准确识图是解题的关键．