题目内容
10.已知:△ABC的两边AB,AC的长关于x的方程x2-(2k+3)x+k2+3k+2=0的两个实数根,第三边BC的长为5.试问:当k取何值时,△ABC是等腰三角形?分析 先求出方程的解,根据两解得出只能BC为腰,分为两种情况,求出即可.
解答 解:x2-(2k+3)x+k2+3k+2=0,
(x-k-1)(x-k-2)=0,
x1=k+1,x2=k+2
所以x1不等于x2,
所以BC为腰,
①当x1=k+1=5时,k=4,
x2=k+2=6;
②当x2=k+2=5时,k=3,
x1=k+1=4,
所以k=4或3.
点评 本题考查了等腰三角形的性质,解一元二次方程的应用,能求出符合条件的所有情况是解此题的关键,用了分类讨论思想.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
20.随着综艺节目“爸爸去哪儿”的热播,问卷调查公司为调查了解该节目在中学生中受欢迎的程度,走进某校园随机抽取部分学生就“你是否喜欢看爸爸去哪儿”进行问卷调查,并将调查结果统计后绘制成如下不完整的统计表:
则a-b=0.1.
| 非常喜欢 | 喜欢 | 一般 | 不知道 | |
| 频数 | 200 | 30 | 10 | |
| 频率 | a | b | 0.025 |
1.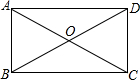 如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )
如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )
 如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )
如图,矩形ABCD中,∠BOC=120°,AB=4,则AC的长是( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 8 |
15.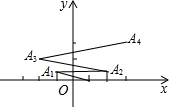 如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
 如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )
如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(-1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(-2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第100次跳动至A100的坐标( )| A. | (50,49) | B. | (51,50) | C. | (-50,49) | D. | (100,99) |
19.一个等腰三角形的一边长是6,另一边长是8.那么这个等腰三角形的周长是( )
| A. | 20 | B. | 20或24 | C. | 22 | D. | 20或22. |
20.-$\frac{1}{2}$的绝对值是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | -2 |
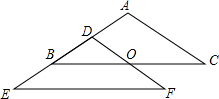 如图所示,△ABC沿直线AB向下平移可以得到△DEF,如果AB=6,BD=4,那么BE=2.
如图所示,△ABC沿直线AB向下平移可以得到△DEF,如果AB=6,BD=4,那么BE=2.