Question

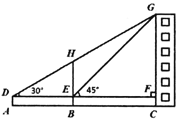
【题目】如图1是一种折叠台灯，将其放置在水平桌面上，图2是其简化示意图，测得其灯臂长为灯翠长为,底座厚度为根据使用习惯，灯臂的倾斜角固定为，

(1)当转动到与桌面平行时,求点到桌面的距离；

(2)在使用过程中发现，当转到至时，光线效果最好，求此时灯罩顶端到桌面的高度(参考数据:，结果精确到个位).

Answer 1

【答案】（1）点到桌面的距离为；（2）灯罩顶端到桌面的高度约为．

【解析】

（1）作CM⊥EF于M，BP⊥AD于P，交EF于N，则CM＝BN，PN＝3，由直角三角形的性质得出AP＝AB＝14，BP＝AP＝14，得出CM＝BN＝BP＋PN＝14＋3即可；

（2）作CM⊥EF于M，作BQ⊥CM于Q，BP⊥AD于P，交EF于N，则∠QBN＝90°，CM＝BN，PN＝3，由（1）得QM＝BN，求出∠CBQ＝25，由三角函数得出CQ＝BC×sin25，得出CM＝CQ＋QM即可．

解当转动到与桌面平行时，

如图2所示:作于于,交于则

，

即点到桌面的距离为;

作于，作于于，交于,如图3所示:

则，

由得

，

在中，

,

即此时灯罩顶端到桌面的高度约为.