题目内容
20.(1)计算:(-$\frac{1}{2}$)-2-|2-$\sqrt{3}$|-3tan30°;(2)解不等式组:$\left\{\begin{array}{l}3x>x+2\\ 4x<3(x+1)\end{array}$.
分析 (1)根据负整数指数幂、绝对值性质及三角函数值计算可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)原式=$4-(2-\sqrt{3})-3×\frac{{\sqrt{3}}}{3}$=4-2+$\sqrt{3}$-$\sqrt{3}$=2;
(2)解不等式①,得x>1,
解不等式②,得x<3,
∴不等式组的解集为1<x<3.
点评 本题考查的是实数的混合运算和解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
15.下列命题中,真命题是( )
| A. | 两条对角线相等的四边形是矩形 | |
| B. | 两条对角线互相垂直且平分的四边形是正方形 | |
| C. | 等边三角形既是轴对称图形又是中心对称图形 | |
| D. | 有一个角是60°的等腰三角形是等边三角形 |
12.某校九年级(1)班全体学生2016年初中毕业体育考试的成绩统计如下表:
根据上表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次考试成绩的众数是28分 | |
| C. | 该班学生这次考试成绩的中位数是28分 | |
| D. | 该班学生这次考试成绩的平均数是28分 |
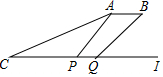 某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93,$\sqrt{3}$≈1.73)
某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援,伤员在C处,直升机在A处,伤员离云梯(AP)150米(即CP的长).伤员从C地前往云梯的同时,直升机受到惯性的影响又往前水平行进50米到达B处,此时云梯也移动到BQ位置,已知∠ACP=30°,∠APQ=60°,∠BQI=43°.问:伤员需前行多少米才能够到云梯?(结果保留整数,sin43°=0.68,cos43°=0.73,tan43°=0.93,$\sqrt{3}$≈1.73)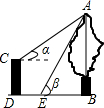 如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号)
如图,CD是一高为4米的平台,AB是与CD底部相平的一棵树,在平台顶C点测得树顶A点的仰角α=30°,从平台底部向树的方向水平前进3米到达点E,在点E处测得树顶A点的仰角β=60°,求树高AB=$\frac{3\sqrt{3}+12}{2}$(结果保留根号)