��Ŀ����
��֪������y=ax2+bx+c�Ķ���Ϊ��1��0������y��Ľ�������Ϊ��0��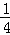 ����R��1��1���������߶Գ���l�ϵ�һ�㣮
����R��1��1���������߶Գ���l�ϵ�һ�㣮
��1����������y=ax2+bx+c�Ľ���ʽ��
��2����P���������ϵ�һ�����㣨��ͼһ������֤����P��R�ľ������P��ֱ��y=﹣1�ľ������ȣ�
��3����ֱ��PR�������ߵ���һ����ΪQ��EΪ�߶�PQ���е㣬����P��E��Q�ֱ���ֱ��y=﹣1�Ĵ��ߣ�����ֱ�ΪM��F��N����ͼ��������֤��PF��QF��
��1���⣺�������߽���ʽΪy=a��x﹣1��2��
�ѣ�0�� �������a=
�������a= ��
��
���������߽���ʽΪy= ��x﹣1��2��
��x﹣1��2��
��2��֤������ͼ1����P��x�� ��x﹣1��2������PM=
��x﹣1��2������PM= ��x﹣1��2+1��
��x﹣1��2+1��
��PR2=��x﹣1��2+[ ��x﹣1��2﹣1]2=��x﹣1��2+[
��x﹣1��2﹣1]2=��x﹣1��2+[ ��x﹣1��]4﹣
��x﹣1��]4﹣ ��x﹣1��2+1=[
��x﹣1��2+1=[ ��x﹣1��]4+
��x﹣1��]4+ ��x﹣1��2+1=[
��x﹣1��2+1=[ ��x﹣1��2+1]2��
��x﹣1��2+1]2��
��PR= ��x﹣1��2+1��
��x﹣1��2+1��
��PR=PM��
����P��R�ľ������P��ֱ��y=﹣1�ľ������ȣ�
��3��֤�����ɣ�2����QN=QR��PR=PM��
��PQ=PR=QR=PM+QN��
��EF��MN��QN��MN��PM��MN��
��EΪ�߶�PQ���е㣬
��EFΪ����PMNQ����λ�ߣ�
��EF= ��QN+PM����
��QN+PM����
��EF= PQ��
PQ��
��EF=EQ=EP��
���F����PQΪֱ����Բ�ϣ�
���PFQ=90�㣬
��PF��QF��


ij����֯��һ�ζ�����ͳ����10��ͬѧ��һ���ڵĶ���ʱ�䣬����һ���ڵĶ���ʱ���ۼ����������10��ͬѧһ�����ۼƶ���ʱ�����λ���ǣ�������
| һ�����ۼƵĶ���ʱ�䣨Сʱ�� | 5 | 8 | 10 | 14 |
| ���������� | 1 | 4 | 3 | 2 |
| �� | A�� | 8 | B�� | 7 | C�� | 9 | D�� | 10 |
ʵ��a��b��c�������϶�Ӧ�ĵ���ͼ��ʾ��������ʽ������ȷ���ǣ�������

| �� | A�� | ac��bc | B�� | |a﹣b|=a﹣b | C�� | ﹣a��﹣b��c | D�� | ﹣a﹣c��﹣b﹣c |
��ͼ��һ���߳�Ϊ4cm�ĵȱ�������ABC�ĸ����O��ֱ����ȣ���O��BC�����ڵ�C����AC�ཻ�ڵ�E����CE�ij�Ϊ��������

| �� | A�� | 4cm | B�� | 3cm | C�� | 2cm | D�� | 1.5cm |
���м�����ȷ���ǣ�������
| �� | A�� | a2•a3=a6 | B�� | ��﹣2ab��2=4a2b2 |
| �� | C�� | ��a2��3=a5 | D�� | 3a2b2��a2b2=3ab |
 ������һ��ֱ�����dz�DEF���ڡ�OAB�ڣ�ʹ��б��FD���߶�AB�ϣ����dz߿������߶�AB���»��������С�EFD=30�㣬ED=2����GΪ��FD���е㣮
������һ��ֱ�����dz�DEF���ڡ�OAB�ڣ�ʹ��б��FD���߶�AB�ϣ����dz߿������߶�AB���»��������С�EFD=30�㣬ED=2����GΪ��FD���е㣮 ��k��0���Ľ���ʽ��
��k��0���Ľ���ʽ��
 ��k��0����ͼ���ϣ�����������������������y1��y2��y3����
��k��0����ͼ���ϣ�����������������������y1��y2��y3����
