题目内容
如图,已知点A(4,0),B(0,4 ),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
),把一个直角三角尺DEF放在△OAB内,使其斜边FD在线段AB上,三角尺可沿着线段AB上下滑动.其中∠EFD=30°,ED=2,点G为边FD的中点.
(1)求直线AB的解析式;
(2)如图1,当点D与点A重合时,求经过点G的反比例函数y= (k≠0)的解析式;
(k≠0)的解析式;
(3)在三角尺滑动的过程中,经过点G的反比例函数的图象能否同时经过点F?如果能,求出此时反比例函数的解析式;如果不能,说明理由.

解:(1)设直线AB的解析式为y=kx+b,
∵A(4,0),B(0,4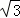 ),
),
∴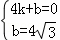 ,
,
解得: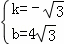 ,
,
∴直线AB的解析式为:y=﹣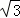 x+4
x+4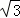 ;
;
(2)∵在Rt△DEF中,∠EFD=30°,ED=2,
∴EF=2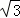 ,DF=4,
,DF=4,
∵点D与点A重合,
∴D(4,0),
∴F(2,2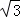 ),
),
∴G(3,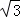 ),
),
∵反比例函数y=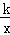 经过点G,
经过点G,
∴k=3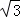 ,
,
∴反比例函数的解析式为:y=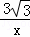 ;
;
(3)经过点G的反比例函数的图象能同时经过点F;理由如下:
∵点F在直线AB上,
∴设F(t,﹣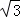 t+4
t+4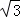 ),
),
又∵ED=2,
∴D(t+2,﹣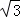 t+2
t+2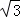 ),
),
∵点G为边FD的中点.
∴G(t+1,﹣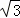 t+3
t+3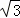 ),
),
若过点G的反比例函数的图象也经过点F,
设解析式为y=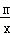 ,
,
则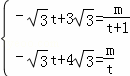 ,
,
整理得:(﹣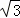 t+3
t+3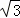 )(t+1)=(﹣
)(t+1)=(﹣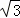 t+4
t+4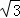 )t,
)t,
解得:t=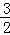 ,
,
∴m=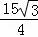 ,
,
∴经过点G的反比例函数的图象能同时经过点F,这个反比例函数解析式为:y=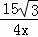 .
.

练习册系列答案
相关题目
在﹣1,﹣2,0,1四个数中最小的数是( )
|
| A. | ﹣1 | B. | ﹣2 | C. | 0 | D. | 1 |
如图,在四边形ABCD中,AB=CD,BA和CD的延长线交于点E,若点P使得S△PAB=S△PCD,则满足此条件的点P( )
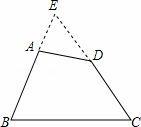
|
| A. | 有且只有1个 |
|
| B. | 有且只有2个 |
|
| C. | 组成∠E的角平分线 |
|
| D. | 组成∠E的角平分线所在的直线(E点除外) |
 +|﹣
+|﹣ |+2sin45°+π0+(
|+2sin45°+π0+( )﹣1.
)﹣1.



 ).
). ).R(1,1)是抛物线对称轴l上的一点.
).R(1,1)是抛物线对称轴l上的一点.
