题目内容
13.(1)已知a、b、c满足2|a-2015|+2c+c2=-1,求c4的值.(2)已知a-b=1,a2+b2=25,求ab的值.
分析 (1)运用配方法把原式和绝对值与偶次方的和的形式,根据非负数的性质解答;
(2)运用完全平方公式进行解答即可.
解答 解:(1)原式变形为:2|a-2015|+2c+c2+1=0,
即2|a-2015|+(c+1)2=0,
则a-2015=0,c+1=0,
解得,a=2015,c=-1,
则c4=-1;
(2)∵a-b=1,
∴(a-b)2=1,
即a2-2ab+b2=1,又a2+b2=25,
∴2ab=24,
则ab=12.
点评 本题考查的是配方法的应用、完全平方公式和非负数的性质,掌握配方法的一般步骤和非负数的性质是解题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
3.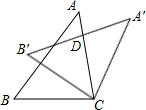 如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
 如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )
如图,把△ABC绕点C顺时针旋转32°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A度数为( )| A. | 48° | B. | 58° | C. | 68° | D. | 78° |
5.方程x2-4x+4=0的根是( )
| A. | x=2 | B. | x1=x2=2 | C. | x=4 | D. | x1=x2=4 |