题目内容
如图(1),四边形AOBC是正方形,点C的坐标是(4
,0),

(1)求点A的坐标点和正方形AOBC的面积;
(2)将正方形绕点O顺时针旋转45°,求旋转后的正方形与原正方形的重叠部分的面积;
(3)如图(2),动点P从点O出发,沿折线O-A-C-B方向以1个单位/每秒匀速运动;另一动点Q从点C出发,沿折线C-B-O-A方向以2个单位/每秒匀速运动.P、Q两点同时出发,当Q运动到点A 时P、Q同时停止运动.设运动时间为t秒,是否存在这样的t值,使△OPQ成为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
| 2 |

(1)求点A的坐标点和正方形AOBC的面积;
(2)将正方形绕点O顺时针旋转45°,求旋转后的正方形与原正方形的重叠部分的面积;
(3)如图(2),动点P从点O出发,沿折线O-A-C-B方向以1个单位/每秒匀速运动;另一动点Q从点C出发,沿折线C-B-O-A方向以2个单位/每秒匀速运动.P、Q两点同时出发,当Q运动到点A 时P、Q同时停止运动.设运动时间为t秒,是否存在这样的t值,使△OPQ成为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.
考点:几何变换综合题
专题:
分析:(1)连接AB,根据△OCA为等腰三角形可得AD=OD的长,从而得出点A的坐标,则得出正方形AOBC的面积;
(2)根据旋转的性质可得OA′的长,从而得出A′C,A′E,再求出面积即可;
(3)存在,从Q点在不同的线段上运动情况,可分为三种:
①当Q点在BC上时,使OQ=QP,则有OP=2BQ,而OP=t,BQ=4-2t,列式可得出t;
②当Q点在OB上时,使OQ=OP,而OP=t,OQ=8-2t,列式可得出t;
③当Q点在OA上时,使OQ=PQ,列式可得出t.
(2)根据旋转的性质可得OA′的长,从而得出A′C,A′E,再求出面积即可;
(3)存在,从Q点在不同的线段上运动情况,可分为三种:
①当Q点在BC上时,使OQ=QP,则有OP=2BQ,而OP=t,BQ=4-2t,列式可得出t;
②当Q点在OB上时,使OQ=OP,而OP=t,OQ=8-2t,列式可得出t;
③当Q点在OA上时,使OQ=PQ,列式可得出t.
解答: 解:(1)如图1,连接AB,与OC交于点D,
解:(1)如图1,连接AB,与OC交于点D,
由△OCA为等腰Rt△,得AD=OD=
OC=2
,
故点A的坐标为(2
,2
),
故正方形AOBC的面积为:
×4
×4
=16;
(2)如图1,旋转后可得OA′=OB=4,
则A′C=4
-4,而可知∠CA′E=90°,∠OCB=45°,
故△A′EC是等腰直角三角形,
则A′E=A′C=4
-4,
故S四边形OA’EB=S△OBC-S△A’EC=16
-16.
(3)存在,从Q点在不同的线段上运动情况,可分为三种:
①如图2,

当Q点在BC上时,使OQ=QP,QM为OP的垂直平分线,
则有OP=2OM=2BQ,而OP=t,BQ=4-2t,
则t=2(4-2t),
解得:t=
.
②如图3,

当Q点在OB上时,使OQ=OP,而OP=t,OQ=8-2t,
则t=8-2t,
解得:t=
.
③当Q点在OA上时,如图4,

使OQ=PQ,t2-24t+96=0,
解得:t=12+4
(舍去),t=12-4
.
 解:(1)如图1,连接AB,与OC交于点D,
解:(1)如图1,连接AB,与OC交于点D,由△OCA为等腰Rt△,得AD=OD=
| 1 |
| 2 |
| 2 |
故点A的坐标为(2
| 2 |
| 2 |
故正方形AOBC的面积为:
| 1 |
| 2 |
| 2 |
| 2 |
(2)如图1,旋转后可得OA′=OB=4,
则A′C=4
| 2 |
故△A′EC是等腰直角三角形,
则A′E=A′C=4
| 2 |
故S四边形OA’EB=S△OBC-S△A’EC=16
| 2 |
(3)存在,从Q点在不同的线段上运动情况,可分为三种:
①如图2,

当Q点在BC上时,使OQ=QP,QM为OP的垂直平分线,
则有OP=2OM=2BQ,而OP=t,BQ=4-2t,
则t=2(4-2t),
解得:t=
| 8 |
| 5 |
②如图3,

当Q点在OB上时,使OQ=OP,而OP=t,OQ=8-2t,
则t=8-2t,
解得:t=
| 8 |
| 3 |
③当Q点在OA上时,如图4,

使OQ=PQ,t2-24t+96=0,
解得:t=12+4
| 3 |
| 3 |
点评:此题考查了正方形的性质,等腰三角形的判定以及旋转的性质,是中考压轴题,综合性较强,难度较大.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目

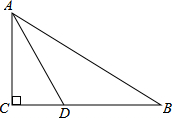 如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,∠BAD=α,sinα=
如图,在Rt△ABC中,∠B=90°,AD平分∠BAC,∠BAD=α,sinα=