题目内容
若一元二次方程ax2=b(ab>0)的两个根分别是m+1与2m-4,则
= .
| b |
| a |
考点:解一元二次方程-直接开平方法
专题:计算题
分析:利用直接开平方法得到x=±
,得到方程的两个根互为相反数,所以m+1+2m-4=0,解得m=1,则方程的两个根分别是2与-2,则有
=2,然后两边平方得到
=4.
|
|
| b |
| a |
解答:解:∵x2=
(ab>0),
∴x=±
,
∴方程的两个根互为相反数,
∴m+1+2m-4=0,解得m=1,
∴一元二次方程ax2=b(ab>0)的两个根分别是2与-2,
∴4a=b
∴
=4.
故答案为:4.
| b |
| a |
∴x=±
|
∴方程的两个根互为相反数,
∴m+1+2m-4=0,解得m=1,
∴一元二次方程ax2=b(ab>0)的两个根分别是2与-2,
∴4a=b
∴
| b |
| a |
故答案为:4.
点评:本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.如果方程化成x2=p的形式,那么可得x=±
;如果方程能化成(nx+m)2=p(p≥0)的形式,那么nx+m=±
.
| p |
| p |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
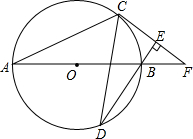 如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.
如图,AB为⊙O直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD.过点C作CE⊥DB,垂足为E,直线AB与CE相交于F点.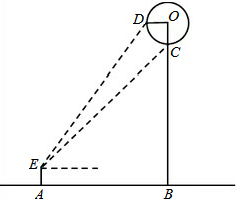 小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)
小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m) 如图,点A在双曲线
如图,点A在双曲线 如图,已知直线l:y=x,过点A1(1,0)作x轴的垂线交直线l于点B1,以A1 B1为边作正方形A1B1C1A2,过点A2作x轴的垂线交直线l于点B2,以A2 B2为边作正方形A2B2C2A3,…;则点A5的坐标为
如图,已知直线l:y=x,过点A1(1,0)作x轴的垂线交直线l于点B1,以A1 B1为边作正方形A1B1C1A2,过点A2作x轴的垂线交直线l于点B2,以A2 B2为边作正方形A2B2C2A3,…;则点A5的坐标为