题目内容
 如图,已知C、D是线段AB上的任意两点,M、N分别是线段AC,BD的中点,MN=20cm,CD=6cm,求线段AB的长.
如图,已知C、D是线段AB上的任意两点,M、N分别是线段AC,BD的中点,MN=20cm,CD=6cm,求线段AB的长.考点:两点间的距离
专题:计算题
分析:先利用线段中点的定义得到MC=
AC,DN=
BD,再利用MC+CD+DN=MN可得AC+BD=28,然后根据AB=AC+CD+BD进行计算即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵M、N分别是线段AC,BD的中点,
∴MC=
AC,DN=
BD,
∵MC+CD+DN=MN,
∴
AC+6+
BD=20,
∴AC+BD=28,
∴AB=AC+CD+BD=AC+BD+CD=28+6=34(cm),
即线段AB的长为34cm.
∴MC=
| 1 |
| 2 |
| 1 |
| 2 |
∵MC+CD+DN=MN,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴AC+BD=28,
∴AB=AC+CD+BD=AC+BD+CD=28+6=34(cm),
即线段AB的长为34cm.
点评:本题考查了两点间的距离:连接两点间的线段的长度叫两点间的距离.距离是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.可以说画线段,但不能说画距离.

练习册系列答案
相关题目
 如图,AC=
如图,AC=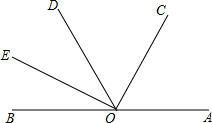 如图,∠AOB为平角,OC平分∠AOD,OE平分∠BOD.
如图,∠AOB为平角,OC平分∠AOD,OE平分∠BOD. 如图,∠ABC=90°,M为AC的中点,CD∥MB,AD⊥CD,点N在CD上,DN=MB,试说明BD与MN的位置关系.
如图,∠ABC=90°,M为AC的中点,CD∥MB,AD⊥CD,点N在CD上,DN=MB,试说明BD与MN的位置关系. 如图,在△ABC中,O是∠ABC与∠ACB外角的平分线BO和CO的交点,则∠BOC与∠A有什么关系?并证明你的结论.
如图,在△ABC中,O是∠ABC与∠ACB外角的平分线BO和CO的交点,则∠BOC与∠A有什么关系?并证明你的结论. 如图,矩形ABCD被两条抛物线截得的阴影部分的面积为4个平方单位,且AB=2,则经过B、O、C三点的抛物线解析式是
如图,矩形ABCD被两条抛物线截得的阴影部分的面积为4个平方单位,且AB=2,则经过B、O、C三点的抛物线解析式是