题目内容
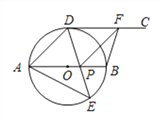
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
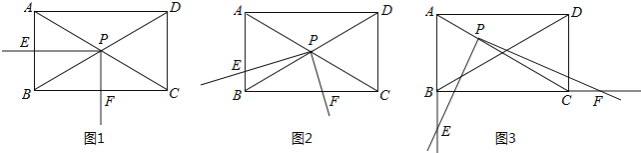
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
【答案】解:(1)![]() 。
。
(2)如答图1,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN。
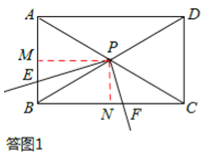
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
由(1)知,![]() ,
,
∴![]() 。
。
(3)变化。证明如下:
如答图2,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN,PM∥BC,PN∥AB。
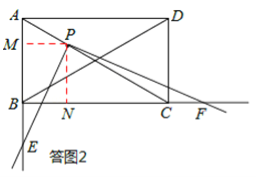
∵PM∥BC,PN∥AB,
∴∠APM=∠PCN,∠PAM=∠CPN。
∴△APM∽△PCN。
∴![]() ,得CN=2PM。
,得CN=2PM。
在Rt△PCN中,![]() ,
,
∴![]() 。
。
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
∴![]() 的值发生变化
的值发生变化
【解析】
试题(1)证明△APE≌△PCF,得PE=CF;在Rt△PCF中,解直角三角形求得![]() 的值:
的值:
∵矩形ABCD,∴AB⊥BC,PA=PC。
∵PE⊥AB,BC⊥AB,∴PE∥BC。∴∠APE=∠PCF。
∵PF⊥BC,AB⊥BC,∴PF∥AB。∴∠PAE=∠CPF。
∵在△APE与△PCF中,∠PAE=∠CPF,PA=PC,∠APE=∠PCF,
∴△APE≌△PCF(ASA)。∴PE=CF。
在Rt△PCF中,![]() ,∴
,∴![]() 。
。
(2)如答图1所示,作辅助线,构造直角三角形,证明△PME∽△PNF,并利用(1)的结论,求得![]() 的值;
的值;
(3)如答图2所示,作辅助线,构造直角三角形,首先证明△APM∽△PCN,求得![]() ;然后证明△PME∽△PNF,从而由
;然后证明△PME∽△PNF,从而由![]() 求得
求得![]() 的值。与(1)(2)问相比较,
的值。与(1)(2)问相比较,![]() 的值发生了变化。
的值发生了变化。