题目内容
1.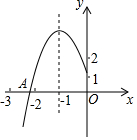 如图所示,抛物线y=ax2+bx+c的顶点为B(-1,3),与x轴的交点A在点(-3,0)和(-2,0)之间,以下结论:
如图所示,抛物线y=ax2+bx+c的顶点为B(-1,3),与x轴的交点A在点(-3,0)和(-2,0)之间,以下结论:①b2-4ac=0;②a+b+c>0;③2a-b=0;④c-a=3
其中正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据抛物线的图象与性质即可判断.
解答 解:抛物线与x轴有两个交点,
∴△>0,
∴b2-4ac>0,故①错误;
由于对称轴为x=-1,
∴x=-3与x=1关于x=-1对称,
∵x=-3时,y<0,
∴x=1时,y=a+b+c<0,故②错误;
∵对称轴为x=-$\frac{b}{2a}$=-1,
∴2a-b=0,故③正确;
∵顶点为B(-1,3),
∴y=a-b+c=3,
∴y=a-2a+c=3,
即c-a=3,故④正确;
故选(B)
点评 本题考查抛物线的图象与性质,解题的关键是熟练运用抛物线的图象与性质,本题属于中等题型.

练习册系列答案
相关题目
11.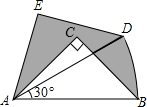 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$-$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
16.下列运算正确的是( )
| A. | |$\sqrt{2}-1$|=$\sqrt{2}-1$ | B. | x3•x2=x6 | C. | x2+x2=x4 | D. | (3x2)2=6x4 |
13. 如图,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α的余角等于( )
如图,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α的余角等于( )
 如图,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α的余角等于( )
如图,直线m∥n,直角三角板ABC的顶点A在直线m上,则∠α的余角等于( )| A. | 19° | B. | 38° | C. | 42° | D. | 52° |
10.下列调查中,最适合采用抽样调查的是( )
| A. | 对某地区现有的16名百岁以上老人睡眠时间的调查 | |
| B. | 对“神舟十一号”运载火箭发射前零部件质量情况的调查 | |
| C. | 对某校九年级三班学生视力情况的调查 | |
| D. | 对某市场上某一品牌电脑使用寿命的调查 |
 如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$.
如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE,连BE,AC=4,BC=2,则BE=$\frac{6\sqrt{5}}{5}$.