化简求值:$\frac{x-1}{{x}^{2}+2x+1}$÷.其中x=$\sqrt{3}$-1．题目和参考答案——青夏教育精英家教网—

题目内容

12．化简求值：$\frac{x-1}{{x}^{2}+2x+1}$÷（1-$\frac{2}{x+1}$），其中x=$\sqrt{3}$-1．

分析原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把已知代入计算即可求出值．

解答解：$\frac{x-1}{{x}^{2}+2x+1}$÷（1-$\frac{2}{x+1}$）=$\frac{x-1}{（x+1）^{2}}$•$\frac{x+1}{x-1}$=$\frac{1}{x+1}$，
∵x=$\sqrt{3}$-1，
∴原式=$\frac{1}{\sqrt{3}-1+1}$=$\frac{\sqrt{3}}{3}$．

点评此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案

相关题目

2．

如图，13个边长为1的小正方形，排列形式如图，把它们分割，使分割后能拼成一个大正方形．请在如图所示的网格中（网格的边长为1）中，用直尺作出这个大正方形．

3．估计$\sqrt{10}$+1的值应在（　　）

20．某地大力发展经济作物，其中果树种植已初具规模，今年受气候、雨水等因素的影响，樱桃较去年有小幅度的减产，而枇杷有所增产．
（1）该地某果农今年收获樱桃和枇杷共400千克，其中枇杷的产量不超过樱桃产量的7倍，求该果农今年收获樱桃至少多少千克？
（2）该果农把今年收获的樱桃、枇杷两种水果的一部分运往市场销售，该果农去年樱桃的市场销售量为100千克，销售均价为30元/千克，今年樱桃的市场销售量比去年减少了m%，销售均价与去年相同；该果农去年枇杷的市场销售量为200千克，销售均价为20元/千克，今年枇杷的市场销售量比去年增加了2m%，但销售均价比去年减少了m%，该果农今年运往市场销售的这部分樱桃和枇杷的销售总金额与他去年樱桃和枇杷的市场销售总金额相同，求m的值．

7．已知x=3是分式方程$\frac{kx}{x-1}$-$\frac{2k-1}{x}$=2的解，那么实数k的值为（　　）

17．已知x₁，x₂是关于x的一元二次方程x²-5x+a=0的两个实数根，且x₁²-x₂²=10，则a=$\frac{21}{4}$．

4．

如图，矩形ABOC的顶点A的坐标为（-4，5），D是OB的中点，E是OC上的一点，当△ADE的周长最小时，点E的坐标是（　　）

1．

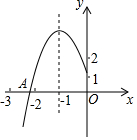如图所示，抛物线y=ax²+bx+c的顶点为B（-1，3），与x轴的交点A在点（-3，0）和（-2，0）之间，以下结论：
①b²-4ac=0；②a+b+c＞0；③2a-b=0；④c-a=3
其中正确的有（　　）个．

2．计算：
（1）（x+y）²-x（2y-x）；
（2）（a+2-$\frac{3a-4}{a-2}$）÷$\frac{{a}^{2}-6a+9}{a-2}$．

试题分类