题目内容
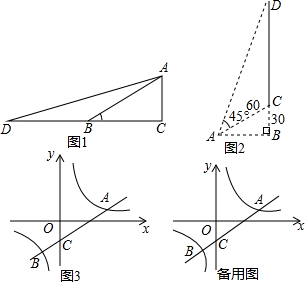
9.将边长为4的等边三角形OAB放置在平面直角坐标系中,其中O为坐标原点,点B在x轴正半轴上,点A在第一象限内,点D是线段OB上的动点,设OD=m.(1)直接写出点B的坐标(4,0).
(2)求△AOD的面积(用含m的代数式表示).
(3)如图1,以AD为直径的⊙M分别交OA、AB于点E、F,连接EF,求线段EF长度的最小值.
(4)如图2,点C为线段AB上的点,且BC=$\frac{1}{3}$AB,点P在线段OA上(不与O、A重合).点D在线段OB上运动,当∠CPD=60°时,求满足条件的点P的个数.

分析 (1)由等边三角形的性质可得OB=4,进而可求出点B的坐标;
(2)易求等边三角形OB边上的高,再利用三角形面积公式即可求出△AOD的面积;
(3)连结EM、FM,作MN⊥EF于N,在等边△OAB中,∠OAB=60°,进而可得EF=2EN=2EM•sin∠EMN=$\frac{{\sqrt{3}}}{2}$AD,若线段EF的长度要最小,则线段AD的长要最小,所以当AD⊥OB时,AD最短,即当m=2时,AD有最小值$2\sqrt{3}$;
(4)利用已知条件易证△OPD∽△ACP,由相似三角形的性质可得:$\frac{OP}{AC}=\frac{OD}{AP}$,设OP=x,则AP=4-x,因为BC=$\frac{1}{3}$AB,所以AC=$\frac{2}{3}$AB=$\frac{8}{3}$,进而$\frac{x}{\frac{8}{3}}$=$\frac{m}{4-x}$,化简得:${x^2}-4x+\frac{8}{3}m=0$,再根据根的判别式即可求出点P的个数.
解答 解:(1)∵△AOB是等边三角形,
∴AO=BO=CO=4,
∴点B的坐标为(4,0),
故答案为:4,0
(2)∵OA=4
∴等边三角形OAB的高为2$\sqrt{3}$,
∴△AOD的面积=$\frac{1}{2}$×2$\sqrt{3}$m=$\sqrt{3}$m;
(3)如图1:连结EM、FM,作MN⊥EF于N,在等边△OAB中,∠OAB=60°,
∴∠EMF=120°,
∵EM=FM,
∴∠EMN=$\frac{1}{2}$∠EMF=60°,
∴EF=2EN=2EM•sin∠EMN=$\frac{{\sqrt{3}}}{2}$AD,
若线段EF的长度要最小,则线段AD的长要最小,
∴当AD⊥OB时,AD最短,
即当m=2时,AD有最小值$2\sqrt{3}$,
此时EF的长度有最小值,最小值为EF=$\frac{{\sqrt{3}}}{2}$×$2\sqrt{3}$=3;
(4)在等边三角形OAB中,∠AOB=∠A=60°,
若∠CPD=60°,则∠APC+∠OPD=120°,
∵∠OPD+∠ODP=120°,
∴∠APC=∠ODP,
∴△OPD∽△ACP,
∴$\frac{OP}{AC}=\frac{OD}{AP}$,
设OP=x,则AP=4-x,
∵BC=$\frac{1}{3}$AB,
∴AC=$\frac{2}{3}$AB=$\frac{8}{3}$,
∴$\frac{x}{\frac{8}{3}}$=$\frac{m}{4-x}$,化简得:${x^2}-4x+\frac{8}{3}m=0$,
∵$△={(-4)^2}-4×1×\frac{8}{3}m=16-\frac{32}{3}m$,
∴当$△<0,即4≥m>\frac{3}{2}时$,方程没有实数根,此时对应的点P不存在;
当$△=0,即m=\frac{3}{2}时$,方程有两个相等的实数根,此时对应的点P有1个;
当$△>0,即0≤m<\frac{3}{2}时$,方程有两个不相等的实数根,此时对应的点P有2个.
点评 本题综合考查了圆的有关知识,用到的知识点有:等边三角形的性质、勾股定理的运用、特殊角的锐角三角函数函数值、相似三角形的判定和性质以及一元二次方程根的判别式,题目的综合性较强,难度中等.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案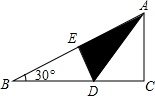 如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )
如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处,已知CD=1,∠B=30°,则BD的长是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
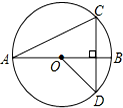 如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )
如图,AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠BOD等于( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
(Ⅰ)根据题意,填写下表:
| 通话时间min | 2 | 3 | 6 | … |
| 通话费用/元 | 2.4 | 2.4 | 5.4 | … |
(Ⅲ)若小红有10元钱,求她打一次电话最多可以通话的时间(本题中通话时间取整数,不足1min的通话时间按1min计费).
| A. | 393×103 | B. | 3.93×103 | C. | 3.93×105 | D. | 3.93×106 |
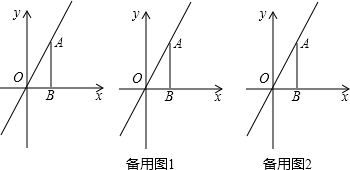
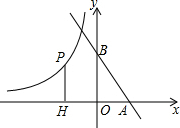 如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.