题目内容
 如图,在?ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
如图,在?ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.
考点:平行四边形的性质,全等三角形的判定与性质
专题:
分析:(1)根据平行四边形的性质和已知条件证明即可;
(2)由菱形的性质可得:BE=DE,因为∠EBD+∠EDB+∠A+∠ABE=180°,所以∠ABD=∠ABE+∠EBD=
×180°=90°,问题得解.
(2)由菱形的性质可得:BE=DE,因为∠EBD+∠EDB+∠A+∠ABE=180°,所以∠ABD=∠ABE+∠EBD=
| 1 |
| 2 |
解答:(1)证明:∵四边形ABCD是平行四边形,
∴∠A=∠C,AD=BC,AB=CD.
∵点E、F分别是AD、BC的中点,
∴AE=
AD,FC=
BC.
∴AE=CF.
在△AEB与△CFD中,
,
∴△AEB≌△CFD(SAS).
(2)解:∵四边形EBFD是菱形,
∴BE=DE.
∴∠EBD=∠EDB.
∵AE=DE,
∴BE=AE.
∴∠A=∠ABE.
∵∠EBD+∠EDB+∠A+∠ABE=180°,
∴∠ABD=∠ABE+∠EBD=
×180°=90°.
∴∠A=∠C,AD=BC,AB=CD.
∵点E、F分别是AD、BC的中点,
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=CF.
在△AEB与△CFD中,
|
∴△AEB≌△CFD(SAS).
(2)解:∵四边形EBFD是菱形,
∴BE=DE.
∴∠EBD=∠EDB.
∵AE=DE,
∴BE=AE.
∴∠A=∠ABE.
∵∠EBD+∠EDB+∠A+∠ABE=180°,
∴∠ABD=∠ABE+∠EBD=
| 1 |
| 2 |
点评:本题考查了平行四边形的性质、全等三角形的判定和性质以及菱形的性质、等腰三角形的判断和性质,题目的综合性较强,难度中等.

练习册系列答案
相关题目
 如图,菱形ABCD中,∠B=60°,点M在AB上,点N在BC上,AM=BN,CM交AN于点P,DP交AC于点Q.求证:
如图,菱形ABCD中,∠B=60°,点M在AB上,点N在BC上,AM=BN,CM交AN于点P,DP交AC于点Q.求证: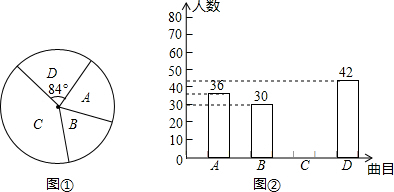


 某校对部分学生家庭进行图书量调查,调查情况如图,若本次调查中,有50本以下图书的学生家庭有24户,则参加本次调查的学生家庭数有
某校对部分学生家庭进行图书量调查,调查情况如图,若本次调查中,有50本以下图书的学生家庭有24户,则参加本次调查的学生家庭数有