题目内容
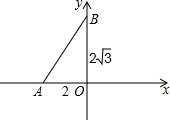 Rt△ABO在平面直角坐标系中的位置如图,AO=2,BO=2
Rt△ABO在平面直角坐标系中的位置如图,AO=2,BO=2| 3 |
考点:相似三角形的判定,坐标与图形性质
专题:
分析:本题可分两种情况:当点D在y轴上时和点D在x轴上时分别讨论,根据射影定理即可求出点D的坐标.
解答:解:在坐标轴上存在点D,使以A,B,D为顶点的三角形与△ABO相似,
理由如下:
当点D在y轴上时则△ABO∽△AD0,
∴AO2=BO•OD,
即4=2
×OD,
∴OD=
,
∴点D的坐标是(0,-
);
当点D在x轴上时则△ABO∽△BD0,
∴BO2=AO•OD,
即12=2×OD,
∴OD=6,
∴点D的坐标是(6,0).
理由如下:
当点D在y轴上时则△ABO∽△AD0,
∴AO2=BO•OD,
即4=2
| 3 |
∴OD=
2
| ||
| 3 |
∴点D的坐标是(0,-
2
| ||
| 3 |
当点D在x轴上时则△ABO∽△BD0,
∴BO2=AO•OD,
即12=2×OD,
∴OD=6,
∴点D的坐标是(6,0).
点评:此题考查了相似三角形的判定与性质、射影定理以及平面直角坐标系中点的坐标特征等知识.此题难度适中,注意数形结合思想与分类讨论思想的应用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是( )
一次函数y=kx+b的图象如图所示,当y>0时,x的取值范围是( )| A、x>2 | B、x<2 |
| C、x>0 | D、x<0 |
 已知:如图,在四边形ABCD中,AB∥DC,BC=b,AB=AC=AD=a,求BD的长.
已知:如图,在四边形ABCD中,AB∥DC,BC=b,AB=AC=AD=a,求BD的长.