题目内容
已知：如图，在四边形ABCD中，AB∥DC，BC=b，AB=AC=AD=a，求BD的长．考点：勾股定理
专题：
分析：以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．在△BDF中，由勾股定理即可求出BD的长．
解答：解：以A为圆心，AB长为半径作圆，延长BA交⊙A于F，连接DF．
∵AB=AC=AD=a，
∴D，C在圆A上，
∵DC∥AB，
∴弧DF=弧BC，
∴DF=CB=b，BF=AB+AF=2AB=2a，
∵FB是⊙A的直径，
∴∠FDB=90°，
∴BD=
=
．
∵AB=AC=AD=a，
∴D，C在圆A上，
∵DC∥AB，
∴弧DF=弧BC，
∴DF=CB=b，BF=AB+AF=2AB=2a，
∵FB是⊙A的直径，
∴∠FDB=90°，
∴BD=
| BF2-DF2 |
| 4a2-b2 |
点评：本题考查了勾股定理，解题的关键是作出以A为圆心，AB长为半径的圆，构建直角三角形，从而求解．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
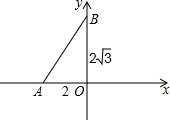Rt△ABO在平面直角坐标系中的位置如图，AO=2，BO=2
采用如下方法可以得到黄金分割点：如图，设AB是已知线段，经过点B作BD⊥AB，使BD=