题目内容

某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y₁（元）与销售月份x（月）满足关系式y₁=- $数学公式$ x+36，而其每千克成本y₂（元）与销售月份x（月）满足函数关系式
y₂= $数学公式$ x²- $数学公式$ x+29 $数学公式$ ．
（1）求出这种水产品每千克的利润y（元）与销售月份x（月）之间的函数关系式．
（2）“五一”之前，几月份出售这种水产品每千克的利润最大？最大利润是多少？

解：（1）∵利润=售价-成本，
∴y=y₁-y₂=- $\text{[math]}$ x+36-（ $\text{[math]}$ x²- $\text{[math]}$ x+29 $\text{[math]}$ ）
=- $\text{[math]}$ x2+ $\text{[math]}$ x+ $\text{[math]}$ ；

（2）y=- $\text{[math]}$ x²+ $\text{[math]}$ x+ $\text{[math]}$ =- $\text{[math]}$ （x-6）²+11，
∵a=- $\text{[math]}$ ＜0，
∴抛物线的开口向下，在对称轴x=6左侧，y随x增大而增大，
∵x＜5，
∴4月份出售利润最大，最大值为- $\text{[math]}$ （4-6）²+11= $\text{[math]}$ ．
分析：（1）根据利润=售价-成本，售价和成本题干已知，列出y与x的函数关系式即可；
（2）由（1）y与x的二次函数关系式，把函数关系式化成顶点坐标式，找出对称轴，求出函数的最大值．
点评：本题主要考查了二次函数的应用的知识点，解答本题的关键熟练掌握二次函数的性质以及二次函数最大值的求解，此题难度不大．

练习册系列答案

同步练习强化拓展系列答案

一课一练天津人民美术出版社系列答案

花山小状元课时练初中生100全优卷系列答案

一课一练文心出版社系列答案

海豚图书中考必备系列答案

授之以渔全国各省市中考试题精选系列答案

中考巨匠系列答案

大舍文化指点中考系列答案

大舍文化中考试题精编系列答案

超能学典中考全面出击系列答案

相关题目

某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y₁（元）与销售月份x（月）满足关系式y=-

x+36，而其每千克成本y₂（元）与销售月

份x（月）满足的函数关系如图所示．
（1）试确定b、c的值；
（2）求出这种水产品每千克的利润y（元）与销售月份x（月）之间的函数关系式；
（3）“五•一”之前，几月份出售这种水产品每千克的利润最大？最大利润是多少？

某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y₁（元）与销售月份x（月）满足关系式y1=-

x+20，而其每千克成本y₂（

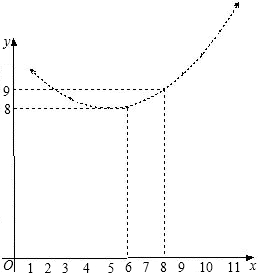元）与销售月份x（月）满足的函数关系y₂=ax²-10ax+c，其图象如图所示．
（1）求y₂的解析式；
（2）问这种水产品下半年几月份出售每千克的利润最大？最大利润是多少？

某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y₁（元）与销售月份x（月）满足关系式y=-

x+36，而其每千克成本y₂（元）与销售月份x（月）满足的函数关系如图所示．
（1）确定这种水产品每千克的利润y（元）与销售月份x（月）之间的函数关系式

；
（2）“五•一”之前，

月份出售这种水产品每千克的利润最大，最大利润是

某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y₁（元）与销售月份x（月）满足关系式y₁=-

x+36，而其每千克成本y₂（元）与销售月份x（月）满足函数关系式
y₂=

．
（1）求出这种水产品每千克的利润y（元）与销售月份x（月）之间的函数关系式．
（2）“五一”之前，几月份出售这种水产品每千克的利润最大？最大利润是多少？

某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价y₁（元）与销售月份x（月）满足关系式

，而其每千克成本y₂（元）与销售月份x（月）满足的函数关系如图所示．
（1）确定这种水产品每千克的利润y（元）与销售月份x（月）之间的函数关系式；
（2）“五•一”之前，月份出售这种水产品每千克的利润最大，最大利润是元．