题目内容
在△ABC中,D、E分别在AB、AC上,AD=4,AB=9,AC=6,则当AE= 时,能使△ABC与△ADE相似.
考点:相似三角形的判定
专题:
分析:由题意可得∠A是公共角,所以利用两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似,判定△ABC与△ADE相似即可,所以可以分别从若①
=
时,△ABC∽△ADE与②若
=
时,△ABC∽△AED去分析求解即可求得答案.
| AB |
| AD |
| AC |
| AE |
| AB |
| AE |
| AC |
| AD |
解答:解:∵在△ABC中,D、E分别在AB、AC上,
∴∠A=∠A,
∵AD=4,AB=9,AC=6,
①若
=
时,△ABC∽△ADE,
即
=
,
解得:AE=
;
②若
=
时,△ABC∽△AED,
即
=
,
解得:AE=6;
∴当AE=
或6时,能使△ABC与△ADE相似.
故答案为:
或6.
∴∠A=∠A,
∵AD=4,AB=9,AC=6,
①若
| AB |
| AD |
| AC |
| AE |
即
| 9 |
| 4 |
| 6 |
| AE |
解得:AE=
| 8 |
| 3 |
②若
| AB |
| AE |
| AC |
| AD |
即
| 9 |
| AE |
| 6 |
| 4 |
解得:AE=6;
∴当AE=
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:此题考查了相似三角形的判定.此题难度适中,解题的关键是注意分类讨论思想的应用,注意掌握两组对应边的比相等且夹角对应相等的两个三角形相似定理的应用.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a6÷a2=a3 |
| B、(a2)3=a8 |
| C、(a2b)3=a6b3 |
| D、a2•a3=a6 |
已知⊙O1的半径是5cm,⊙O2的半径是2cm,O1O2=3cm,则两圆的位置关系是( )
| A、外离 | B、内切 | C、相交 | D、内含 |
 如图,矩形ABCD中,AB=3,BC=6.分别以B、D为圆心,AB为半径画弧,两弧分别交对角线BD于点E、F,则图中阴影部分的面积为
如图,矩形ABCD中,AB=3,BC=6.分别以B、D为圆心,AB为半径画弧,两弧分别交对角线BD于点E、F,则图中阴影部分的面积为 如图,△ABC的面积为3,∠B=15°,点D在边BC上,DA⊥AB.设BC=x,BD=y.则y关于x的函数解析式为
如图,△ABC的面积为3,∠B=15°,点D在边BC上,DA⊥AB.设BC=x,BD=y.则y关于x的函数解析式为 到琴弦.(答案需为整数)
到琴弦.(答案需为整数)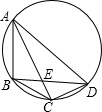 如图,A、B、C、D在同一圆周上,AC与BD交于E,且BC=CD=2,AE=3,则CE的长是
如图,A、B、C、D在同一圆周上,AC与BD交于E,且BC=CD=2,AE=3,则CE的长是