��Ŀ����
15����ͼ�ף���֪����ABCD�У�AD��BC����D=90�㣬BC=5��CD=3��cotB=1��P�DZ�BC�ϵ�һ�����㣨�����B����C�غϣ�������P������PE��ʹ����PE������BA�ڵ�E����BPE=��CPD����1����ͼ�ң�����E���A�غ�ʱ�����DPC������ֵ��
��2������E�����߶�AB��ʱ����BP=x��BE=y������y��x֮��ĺ�������ʽ����д��x��ȡֵ��Χ��
��3������BE��Ϊ�뾶�ġ�B����AD��Ϊֱ���ġ�O���У���BP�ij���
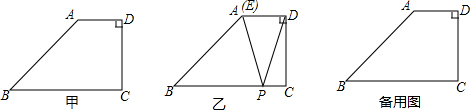
���� ��1����AH��BC��H��֤����AHP�ա�DCP�����PC�ij����õ���DPC������ֵ��
��2����EM��BC��M����x��y��ʾBM��PM��֤����EPM�ס�DPC���õ�y��x֮��ĺ�������ʽ��
��3���ֵ�E���߶�AB�Ϻ��߶�AB���ӳ��������������������Բ����ʱ��Բ�ľ�����Բ�뾶�Ĺ�ϵ��ɣ�
��� �⣺��1����ͼ1����AH��BC��H��
�ڡ�AHP�͡�DCP�У�
$\left\{\begin{array}{l}{��BPF=��CPD}\\{��AHP=��DCP}\\{AH=DC}\end{array}\right.$
���AHP�ա�DCP��AAS����
��HP=PC
��cotB=1��
���B=45�㣬BH=AH=3��HP=PC=1��
tan��DPC=3
��2����ͼ2����EM��BC��M��
EM=BM=$\frac{\sqrt{2}}{2}$y��PM=x-$\frac{\sqrt{2}}{2}$y��
��EPM�ס�DPC��
��$\frac{EM}{CD}$=$\frac{PM}{CP}$
$\frac{\frac{\sqrt{2}}{2}y}{3}$=$\frac{x-\frac{\sqrt{2}}{2}y}{5-x}$��y=$\frac{3\sqrt{2}x}{8-x}$��0��x��4��
��3����ͼ3��
��OΪAD���е㣬
��BO=5��
��E�ڱ�AB��ʱ��BO=BE+AO
5=1+$\frac{3\sqrt{2}x}{8-x}$��BP=x=48$\sqrt{2}$-64��
��E�ڱ�AB�ӳ�����ʱ��BO=BE-AO
5=$\frac{3\sqrt{2}x}{8-x}$-1��BP=x=16-8$\sqrt{2}$
���� ���⿼�����ֱ�����Ρ����������Ρ�������Ǻ�������Բ���е�֪ʶ���ۺ��Խ�ǿ����Ҫѧ�����ۺ�����֪ʶ���������Ͻ�����˼ά���������ʱ��ע�����ν��˼��ͷ�������˼������ã�

 Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д� ���������������Բ��������ϵ�д�
���������������Բ��������ϵ�д�| A�� | 3 | B�� | 3x3 | C�� | 3x4 | D�� | 3x3 |
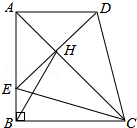 ���ı���ABCD�У�AD��BC����ABC=90�㣬AB=BC��EΪAB����һ�㣬��BCE=15�㣬��AE=AD������DE���Խ���AC��H������BH��
���ı���ABCD�У�AD��BC����ABC=90�㣬AB=BC��EΪAB����һ�㣬��BCE=15�㣬��AE=AD������DE���Խ���AC��H������BH��