题目内容
关于x的一元二次方程mx2-3x-4=4x+3有实数根,则m的取值范围是( )
A、m>-
| ||
B、m≤-
| ||
C、m≥-
| ||
D、m≥-
|
考点:根的判别式,一元二次方程的定义
专题:
分析:首先化为一般形式,进一步利用判别式和一元二次方程根的关系求解即可.
解答:解:由mx2-3x-4=4x+3得
mx2-7x-7=0,
m≠0,要使x的一元二次方程mx2-7x-7=0有实根,
则判别式△=(-7)2-4×m×(-7)≥0,
整理得49+28m≥0,解得m≥-
,且m≠0.
故选:D.
mx2-7x-7=0,
m≠0,要使x的一元二次方程mx2-7x-7=0有实根,
则判别式△=(-7)2-4×m×(-7)≥0,
整理得49+28m≥0,解得m≥-
| 7 |
| 4 |
故选:D.
点评:本题主要考查判别式和二次方程根的对应关系,主要二次项系数不能为0.

练习册系列答案
相关题目
民间剪纸在我国有着悠久的历史,下列图案是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
若不等式组
的整数解共有三个,则a的整数值为( )
|
| A、4 | B、5 | C、6 | D、7 |
袋中有4个红球,x个黄球,从中任摸一个恰为黄球的概率为
,则x为( )
| 3 |
| 4 |
| A、9 | B、12 | C、10 | D、16 |
人们都是知道“五角星☆”的五个角的相等,那么每一个角的度数是( )
| A、60° | B、45° |
| C、36° | D、30° |
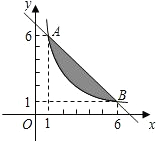 如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y=
如果一个点的横、纵坐标均为整数,那么我们称这个点是格点,如图,A、B两点在函数y= △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示.