题目内容
15.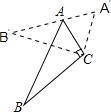 如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C′,且点A在A′B′上,则旋转角为50°.
如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C′,且点A在A′B′上,则旋转角为50°.
分析 由将△ACB绕点C顺时针旋转得到△A′B′C′,即可得△ACB≌△A′B′C′,则可得∠A'=∠BAC,△AA'C是等腰三角形,又由△ACB中,∠ACB=90°,∠ABC=25°,即可求得∠A'、∠B'AB的度数,即可求得∠ACB'的度数,继而求得∠B'CB的度数.
解答 解:∵将△ACB绕点C顺时针旋转得到△A′B′C′,
∴△ACB≌△A′B′C′,
∴∠A'=∠BAC,AC=CA',
∴∠BAC=∠CAA',
∵△ACB中,∠ACB=90°,∠ABC=25°,
∴∠BAC=90°-∠ABC=65°,
∴∠BAC=∠CAA'=65°,
∴∠B'AB=180°-65°-65°=50°,
∴∠ACB'=180°-25°-50°-65°=40°,
∴∠B'CB=90°-40°=50°.
故答案为:50°.
点评 此题考查了旋转的性质、直角三角形的性质以及等腰三角形的性质.此题难度不大,注意掌握旋转前后图形的对应关系,注意数形结合思想的应用.

练习册系列答案
相关题目
3.已知弹簧在一定限度内,它的长度y(厘米)与所挂重物质量x(千克)是一次函数关系.表中记录的是两次挂不同重量重物的质量(在弹性限度内)与相对应的弹簧长度.
求不挂重物时弹簧的长度.
| 所挂重物质量x(千克) | 2.5 | 5 |
| 弹簧长度y(厘米) | 7.5 | 9 |
7. 下面所给几何体的俯视图是( )
下面所给几何体的俯视图是( )
 下面所给几何体的俯视图是( )
下面所给几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
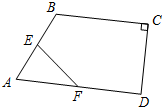 已知:如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=6,CD=4,则EF=$\sqrt{13}$.
已知:如图,在四边形ABCD中,∠C=90°,E、F分别为AB、AD的中点,BC=6,CD=4,则EF=$\sqrt{13}$.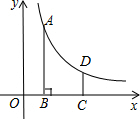 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD=$\frac{4}{3}$
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$(x>0)的图象上有一点A(m,4),过点A作AB⊥x轴于点B,将点B向右平移2个单位长度得到点C,过点C作y轴的平行线交反比例函数的图象于点D,CD=$\frac{4}{3}$ 如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A(1,0)、B(3,0)两点,与y轴交于点C,其顶点为点D,点E的坐标为(0,-1),该抛物线与BE交于另一点F,连接BC.