题目内容
6.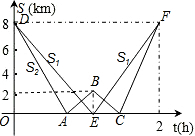 在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),下图中的折线分别表示S1、S2与t之间的函数关系.
在一次远足活动中,某班学生分成两组,第一组由甲地匀速步行到乙地后原路返回,第二组由甲地匀速步行经乙地继续前行到丙地后原路返回,两组同时出发,设步行的时间为t(h),两组离乙地的距离分别为S1(km)和S2(km),下图中的折线分别表示S1、S2与t之间的函数关系.(1)甲、乙两地之间的距离为8km,乙、丙两地之间的距离为2km;
(2)求第二组由甲地出发首次到达乙地及由乙地到达丙地所用的时间分别是多少?
(3)求图中线段AB所表示的S2与t间的函数关系式,并写出自变量t的取值范围.
(4)求线段AB和DE的交点P的坐标,并说明P点坐标的实际意义.
分析 (1)根据函数图象知道当S=0时表示从甲地到了乙地,由此可以得到甲、乙两地之间的距离,同样的方法得到乙、丙两地之间的距离;
(2)由图象可知,第二组一共走了2小时,总路程为8+2+2+8=20千米,即其速度为10千米/时,而其由甲地出发首次到乙地所走的路程为8千米,由乙地到丙地的路程为2千米,利用时间=路程÷速度即可求出两个时间;
(3)由(2)可知,A(0.8,0),B(0.2+0.8,2),设s2=kt+b,将A、B两点的坐标代入,建立方程组,即可求解;
(4)先根据待定系数法得到DE的函数解析式,联立线段AB和线段DE的函数关系式,可得交点P的坐标,进一步即可求解.
解答 解:(1)根据图象知道:甲、乙两地之间的距离为8km,乙、丙两地之间的距离为2km.
故答案为:8,2;
(2)第二组由甲地出发首次到达乙地所用的时间为
8÷[2×(8+2)÷2]=8÷10=0.8(小时)
第二组由乙地到达丙地所用的时间为
2÷[2×(8+2)÷2]=2÷10=0.2(小时);
(3)根据题意得A、B的坐标分别为(0.8,0)和(1,2)
设线段AB的函数关系式为:S2=kt+b
根据题意,得
$\left\{\begin{array}{l}{0=0.8k+b}\\{2=k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=10}\\{b=-8}\end{array}\right.$.
故图中线段AB所表示的S2与t间的函数关系式为S2=10t-8,自变量t的取值范围是0.8≤t≤1.
(4)根据题意得D、B的坐标分别为(0,8)和(1,0)
设线段DE的函数关系式为:S1=kt+b
根据题意,得
$\left\{\begin{array}{l}{b=8}\\{k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-8}\\{b=8}\end{array}\right.$.
故图中线段de所表示的S2与t间的函数关系式为S1=-8t+8;
联立线段AB和线段DE的函数关系式,
则交点P的坐标:$(\frac{8}{9},\frac{8}{9})$.
当t=$\frac{8}{9}$小时时,第一组和第二组与乙地的距离都是$\frac{8}{9}$千米,但并非相遇.
点评 考查了一次函数的应用,本题关键是仔细分析题意,结合图象,利用待定系数法才可解决问题.解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.

 天天向上口算本系列答案
天天向上口算本系列答案| A. | 12x=18(28-x) | B. | 2×12x=18(28-x) | C. | 2×18x=12(28-x) | D. | 12x=2×18(28-x) |
| A. | 4x-1=3x | B. | 2x-2=3x+3 | C. | 3x+2=2x-1 | D. | 4x-3=3x-1 |
| A. | ax2+bx+c=0 | B. | |a|x2+bx+c=0 | C. | $\sqrt{a}$x2+bx+c=0 | D. | (a2+1)x2+bx+c=0 |
 如图所示,在直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(2,3),B(5,4),C(8,2),试确定这个四边形的面积.
如图所示,在直角坐标系中,四边形OABC各顶点的坐标分别是O(0,0),A(2,3),B(5,4),C(8,2),试确定这个四边形的面积.