Question

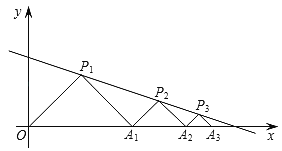
【题目】如图，在平面直角坐标系中，△P1OA1，△P2A1A2，△P3A2A3，…都是等腰直角三角形，其直角顶点P1（3，3），P2，P3，…均在直线y＝﹣x+4上．设△P1OA1，△P2A1A2，△P3A2A3，…的面积分别为S1，S2，S3，…，根据图形所反映的规律，S2019＝（　　）

A.B.C.D.

Answer 1

【答案】A

【解析】

分别过点P1、P2、P3作x轴的垂线段，先根据等腰直角三角形的性质求得前三个等腰直角三角形的底边和底边上的高，继而求得三角形的面积，得出面积的规律即可得出答案．

解：如图，分别过点P1、P2、P3作x轴的垂线段，垂足分别为点C、D、E，

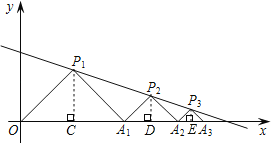
∵P1（3，3），且△P1OA1是等腰直角三角形，

∴OC＝CA1＝P1C＝3，

设A1D＝a，则P2D＝a，

∴OD＝6+a，

∴点P2坐标为（6+a，a），

将点P2坐标代入y＝﹣x+4，得：﹣（6+a）+4＝a，

解得：a＝，

∴A1A2＝2a＝3，P2D＝，

同理求得P3E＝、A2A3＝，

∵S1＝×6×3＝9×（）0、S2＝×3×＝9×（）、

S3＝××＝9×（）2、……

∴S2019＝9×（）2018．

故选：A．