Question

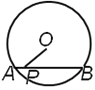
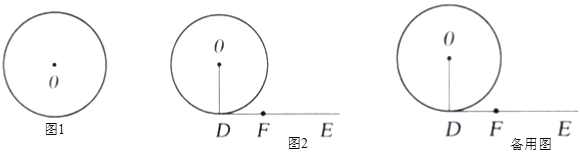
【题目】（1）①如图1，请用直尺（不带刻度）和圆规作出的内接正三角形（按要求作图，不要求写作法，但要保留作图痕迹）.

②若的内接正三角形边长为6，求的半径；

（2）如图2，的半径就是（1）中所求半径的值.点在上，是的切线，点在射线上，且，点从点出发，以每秒1个单位的速度沿射线方向移动，点是上的点（不与点重合），是的切线.设点运动的时间为（秒），当为何值时，是直角三角形，请你求出满足条件的所有值.

Answer 1

【答案】（1）①见解析；②；（2）.

【解析】

（1）①作半径的垂直平分线与圆交于，再取，则即为正三角形；

②连接，设半径为，利用勾股定理即可求得答案；

（2）分当，且点在点左侧或右侧，时四种情况讨论，当时，在Rt中利用勾股定理求解即可；当且点在点左侧或右侧时，构造矩形和直角三角形，利用解直角三角形即可求解；当时，构造正方形和直角三角形即可求解.

（1）①等边如图所示；

②连接，如图，设半径为，

由作图知：，⊥，

∴，

在中，

，即，

解得：；

（2）当时，连接，如图，

∵QG是的切线，

∴，

∵，

∴三点共线，

又∵DF是的切线，

∴，

设点运动的时间为（秒），

∴，

在中，，，

∴，

在Rt中，，，，

∴，即，

解得：；

当，且点在点左侧时，连接，过点G作GM⊥OD于M，如图，

∵是的切线，

∴，

∴四边形DFGM为矩形，

∴，

在Rt中，，，

∴，

∵，

∴，

∵QG是的切线，四边形DFGM为矩形，

∴，

∴

在Rt中，，，

∴即

解得：；

当时，连接，如图，

∵是的切线，QG是的切线，

∴，，

∴四边形ODQG为正方形，

∴，

∴；

当，且点在点左侧时，连接，过点O作ON⊥于N，如图，

∵是的切线，

∴，

∴四边形DFNO为矩形，

∴，

在Rt中，，，

∴，

∵，

∴，

∴，，

∴，

∵QG是的切线，

，

∴，

∴，

∴，

∴；

综上：当、、、时，是直角三角形.