题目内容
10.观察下列算式:$\frac{1}{\sqrt{2}+1}$=$\frac{(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\frac{(\sqrt{2}-1)}{1}$=$\sqrt{2}-1$$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\frac{\sqrt{3}-\sqrt{2}}{1}$=$\sqrt{3}-\sqrt{2}$
$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\frac{(\sqrt{4}-\sqrt{3})}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$=$\frac{\sqrt{4}-\sqrt{3}}{1}$=$\sqrt{4}-\sqrt{3}$
(1)根据你发现的规律填空:$\frac{1}{\sqrt{2015}+\sqrt{2014}}$=$\sqrt{2015}$-$\sqrt{2014}$,$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$.
(2)对比下面的算式与上面的有何异同,根据你的观察、猜想与验证,计算:
($\frac{1}{\sqrt{3}+1}+$$\frac{1}{\sqrt{5}+\sqrt{3}}$+$\frac{1}{\sqrt{7}+\sqrt{5}}$…+$\frac{1}{\sqrt{2015}+\sqrt{2013}}$)×($\sqrt{2015}+1$)
分析 (1)根据得出的分母有理化规律将各式化简即可;
(2)原式利用分母有理化方法变形,计算即可得到结果.
解答 解:(1)$\frac{1}{\sqrt{2015}+\sqrt{2014}}$=$\sqrt{2015}$-$\sqrt{2014}$,$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$.
故答案为:$\sqrt{2015}$-$\sqrt{2014}$;$\sqrt{n}$-$\sqrt{n-1}$.
(2)∵$\frac{1}{\sqrt{3}+1}$=$\frac{\sqrt{3}-1}{(\sqrt{3}+1)(\sqrt{3}-1)}$=$\frac{1}{2}$($\sqrt{3}$-1),$\frac{1}{\sqrt{5}+\sqrt{3}}$=$\frac{\sqrt{5}-\sqrt{3}}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}$=$\frac{1}{2}$($\sqrt{5}$-$\sqrt{3}$),$\frac{1}{\sqrt{7}+\sqrt{5}}$=$\frac{\sqrt{7}-\sqrt{5}}{(\sqrt{7}+\sqrt{5})(\sqrt{7}-\sqrt{5})}$=$\frac{1}{2}$($\sqrt{7}$-$\sqrt{5}$),…,
∴$\frac{1}{\sqrt{2n+1}-\sqrt{2n-1}}$=$\frac{1}{2}$($\sqrt{2n+1}$-$\sqrt{2n-1}$)(n为正整数).
∴原式=[$\frac{1}{2}$($\sqrt{3}$-1)+$\frac{1}{2}$($\sqrt{5}$-$\sqrt{3}$)+$\frac{1}{2}$($\sqrt{7}$-$\sqrt{5}$)+…+$\frac{1}{2}$($\sqrt{2015}$-$\sqrt{2013}$)]×($\sqrt{2015}$+1),
=$\frac{1}{2}$($\sqrt{3}$-1+$\sqrt{5}$-$\sqrt{3}$+$\sqrt{7}$-$\sqrt{5}$+…+$\sqrt{2015}$-$\sqrt{2013}$)×($\sqrt{2015}$+1),
=$\frac{1}{2}$($\sqrt{2015}$-1)×($\sqrt{2015}$+1),
=1007.
点评 本题考查了分母有理化,解题的关键是:(1)根据给定的等式找出$\frac{1}{\sqrt{n}+\sqrt{n-1}}$=$\sqrt{n}$-$\sqrt{n-1}$;(2)根据分母有理化方法找出$\frac{1}{\sqrt{2n+1}-\sqrt{2n-1}}$=$\frac{1}{2}$($\sqrt{2n+1}$-$\sqrt{2n-1}$)(n为正整数).

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | a•a3=a3 | B. | (ab)3=a3b3 | C. | (a3)2=a5 | D. | -3a-a=-2a |
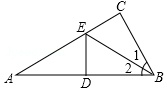 如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于6cm.
如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于6cm. 如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=$\frac{1}{3}$;若S△ABC=12,则S△ADF-S△BEF=2.
如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=$\frac{1}{3}$;若S△ABC=12,则S△ADF-S△BEF=2.