题目内容
2.数学老师布置了一道思考题“计算:(-$\frac{1}{12}$)$÷(\frac{1}{3}-\frac{5}{6})$”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.小明的解法:原式的倒数为($\frac{1}{3}-\frac{5}{6}$)$÷(-\frac{1}{12})$=($\frac{1}{3}-\frac{5}{6}$)×(-12)=-4+10=6,
所以(-$\frac{1}{12}$)$÷(\frac{1}{3}-\frac{5}{6})$=$\frac{1}{6}$.
(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-$\frac{1}{24}$)$÷(\frac{1}{3}-\frac{1}{6}+\frac{3}{8})$.
分析 (1)正确,利用倒数的定义判断即可;
(2)求出原式的倒数,即可确定出原式的值.
解答 解:(1)正确,理由为:一个数的倒数的倒数等于原数;
(2)原式的倒数为($\frac{1}{3}$-$\frac{1}{6}$+$\frac{3}{8}$)÷(-$\frac{1}{24}$)=($\frac{1}{3}$-$\frac{1}{6}$+$\frac{3}{8}$)×(-24)=-8+4-9=-13,
则(-$\frac{1}{24}$)÷($\frac{1}{3}$-$\frac{1}{6}$+$\frac{3}{8}$)=-$\frac{1}{13}$.
点评 此题考查了有理数的除法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
13.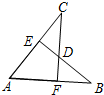 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.
以上结论正确的( )
 如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上.
以上结论正确的( )
| A. | 只有① | B. | 只有② | C. | 只有③ | D. | 有①和②和③ |
17.观察下表,确定一元二次方程x2-2x-2=0的一个近似根.
| x | 2.1 | 2.2 | 2.3 | 2.4 | 2.5 | 2.6 | 2.7 | 2.8 |
| x2-2x-2 | -1.79 | -1.56 | -1.31 | -1.04 | -0.75 | -0.44 | -0.11 | 0.24 |
7.已知圆弧的度数为120°,弧长为6πcm,则圆的半径为( )
| A. | 6cm | B. | 9cm | C. | 12cm | D. | 15cm |
 a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是③④.
a,b,c三个数在数轴上的位置如图所示,则下列结论中错误的是③④.