题目内容
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,对角线AC与BD相交于点O,线段OA,OB的中点分别为E,F.
(1)求证:△FOE≌△DOC;
(2)求sin∠OEF的值;
(3)若直线EF与线段AD,BC分别相交于点G,H,求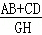 的值.
的值.
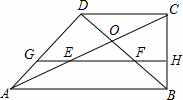
(1)证明:∵EF是△OAB的中位线,
∴EF∥AB,EF= AB,
AB,
而CD∥AB,CD= AB,
AB,
∴EF=CD,∠OEF=∠OCD,∠OFE=∠ODC,
∴△FOE≌△DOC;
(2)解:∵EF∥AB,
∴∠OEF=∠CAB,
∵在Rt△ABC中,AC= =
= =
= BC,
BC,
∴sin∠OEF=sin∠CAB= =
= =
= ;
;
(3)解:∵AE=OE=OC,EF∥CD,
∴△AEG∽△ACD,
∴ =
= =
= ,即EG=
,即EG= CD,
CD,
同理FH= CD,
CD,
∴ =
= =
= .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )厘米的正方形,利用因式分解计算当a=13.2,b=3.4时,剩余部分的面积。
)厘米的正方形,利用因式分解计算当a=13.2,b=3.4时,剩余部分的面积。
 ,则tan
,则tan = .
= . ,其中a满足方程a2+4a+1=0.
,其中a满足方程a2+4a+1=0.
 的最大真分数是( ),最小假分数是( ),把这个假分数再添上( )个这样的分数单位就是最小的素数.
的最大真分数是( ),最小假分数是( ),把这个假分数再添上( )个这样的分数单位就是最小的素数.