题目内容
11.若方程(a+1)x2-3x+1=0是关于x的一元二次方程,则a需满足a≠-1.分析 只含有一个未知数,并且所含未知数的项的最高次数是2的整式方程叫一元二次方程,根据以上定义得出a+1≠0,求出即可.
解答 解:∵方程(a+1)x2-3x+1=0是关于x的一元二次方程,
∴a+1≠0,
∴a≠-1,
故答案为:a≠-1.
点评 本题考查了一元二次方程的定义的应用,能理解一元二次方程的定义是解此题的关键.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
1.若关于x一元二次方程x2-4x+c=0的两根为x1、x2,且x12-x1x2=0,则c的值是( )
| A. | 0 | B. | 4 | C. | 0或4 | D. | 0或-4 |
2.如果关于x的方程ax2+x-1=0有两个实数根,则a的取值范围是( )
| A. | a>-$\frac{1}{4}$ | B. | a≥-$\frac{1}{4}$ | C. | a≥-$\frac{1}{4}$且a≠0 | D. | a>-$\frac{1}{4}$且a≠0 |
6.当b+c=0时,二次函数y=x2+bx+c的图象一定经过点( )
| A. | (-1,-1) | B. | (1,-1) | C. | (-1,1) | D. | (1,1) |
3.若点C为线段AB的黄金分割点,则下列式子正确的是( )
| A. | $\frac{AC}{BC}$=$\frac{AB}{AC}$ | B. | $\frac{AC}{AB}$=$\frac{AB}{BC}$ | C. | $\frac{AB}{AC}$=$\frac{-1+\sqrt{5}}{2}$ | D. | $\frac{AB}{BC}$=$\frac{-1+\sqrt{5}}{2}$ |
20.已知A(-2,y1)、B(-1,y2)、C(3,y3)都在反比例函数y=-$\frac{2}{x}$的图象上,则y1、y2、y3大小关系正确的是( )
| A. | y2>y1>y3 | B. | y1>y2>y3 | C. | y3>y1>y2 | D. | y3>y2>y1 |
1.下列各式一定是二次根式的是( )
| A. | $\sqrt{a}$ | B. | $\root{3}{2}$ | C. | $\sqrt{-3}$ | D. | -$\sqrt{7}$ |
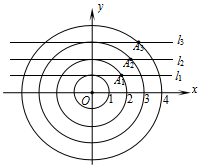 如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点A12的坐标为(5,12).
如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点A12的坐标为(5,12). 如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.
如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.