题目内容
19.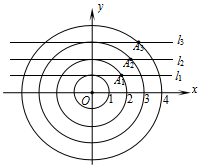 如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点A12的坐标为(5,12).
如图,在平面直角坐标系中,点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点;点A2是以原点O为圆心,半径为3的圆与过点(0,2)且平行于x轴的直线l2的一个交点;…按照这样的规律进行下去,点A12的坐标为(5,12).
分析 根据题意,可以首先求得A1($\sqrt{3}$,1),A2($\sqrt{5}$,2),A3($\sqrt{7}$,3).根据这些具体值,不难发现:An的纵坐标是n,横坐标是$\sqrt{2n+1}$.
解答 解:∵点A1是以原点O为圆心,半径为2的圆与过点(0,1)且平行于x轴的直线l1的一个交点,
∴A1的纵坐标为1,横坐标为:$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,即A1($\sqrt{3}$,1);
同理可求:A2($\sqrt{5}$,2),A3($\sqrt{7}$,3)
∴根据这些具体值,得出规律:An的纵坐标是n,横坐标是$\sqrt{2n+1}$.即An的坐标为($\sqrt{2n+1}$,n),
当n=12时,A12的坐标为(5,12),
故答案为:(5,12).
点评 此题考查了点的坐标变化规律和勾股定理,可以首先求得几个具体值,然后进一步发现坐标和脚码的规律.

练习册系列答案
相关题目
9.室内温度10℃,室外温度是-1℃,那么室内温度比室外温度高( )
| A. | -11℃ | B. | -9℃ | C. | 9℃ | D. | 11℃ |
7.如果3x3yn+(m-2)x是关于x、y的五次二项式,则m、n的值为( )
| A. | m=3,n=2 | B. | m≠2,n=2 | C. | m为任意数,n=2 | D. | m≠2,n=3 |
14.下列算式,结果最小的是( )
| A. | 1+(-1) | B. | 1-(-2) | C. | 1×(-2) | D. | 1÷(-2) |
9.抛掷一枚硬币,出现正面和反面的概率为( )
| A. | 都为$\frac{1}{2}$ | B. | 都为1 | C. | 都为$\frac{1}{4}$ | D. | 都为$\frac{1}{8}$ |