МвДҝДЪИЭ
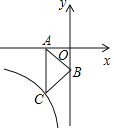
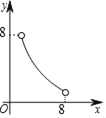
ЎҫМвДҝЎҝИзНјЈ¬Т»ҙОәҜКэyЈҪx©Ғ3өДНјПуУл·ҙұИАэәҜКэyЈҪ![]() ЈЁkЎЩ0Ј©өДНјПуҪ»УЪөгAУлөгBЈЁaЈ¬©Ғ4Ј©Ј®
ЈЁkЎЩ0Ј©өДНјПуҪ»УЪөгAУлөгBЈЁaЈ¬©Ғ4Ј©Ј®

ЈЁ1Ј©Зу·ҙұИАэәҜКэөДұнҙпКҪЈ»
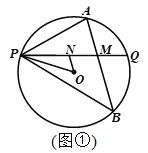
ЈЁ2Ј©Т»ҙОәҜКэyЈҪx©Ғ3өДНјПуУлxЦбҪ»УЪөгMЈ¬Б¬ҪУOBЈ¬ЗуЎчOBMөДГж»эЈ»
ЈЁ3Ј©Иф¶ҜөгPКЗөЪТ»ПуПЮДЪЛ«ЗъПЯЙПөДөгЈЁІ»УлөгAЦШәПЈ©Ј¬Б¬ҪУOPЈ¬ЗТ№эөгPЧчyЦбөДЖҪРРПЯҪ»ЦұПЯABУЪөгCЈ¬Б¬ҪУOCЈ¬ИфЎчPOCөДГж»эОӘ3Ј¬ЗлЦұҪУРҙіцөгPөДЧшұкЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©yЈҪ![]() Ј»ЈЁ2Ј©ЎчOBMөДГж»эОӘ6Ј»ЈЁ3Ј©өгPөДЧшұкОӘЈЁ5Ј¬
Ј»ЈЁ2Ј©ЎчOBMөДГж»эОӘ6Ј»ЈЁ3Ј©өгPөДЧшұкОӘЈЁ5Ј¬![]() Ј©»тЈЁ1Ј¬4Ј©»тЈЁ2Ј¬2Ј©Ј®
Ј©»тЈЁ1Ј¬4Ј©»тЈЁ2Ј¬2Ј©Ј®
ЎҫҪвОцЎҝ
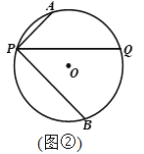
ЈЁ1Ј©ёщҫЭөгBФЪТ»ҙОәҜКэЙПҝЙТФЗуіцөгBөДЧшұкЈ¬ФЪҪ«өгBҙъИл·ҙұИАэәҜКэЦРјҙҝЙЗуіц·ҙұИАэұнҙпКҪЈ»
ЈЁ2Ј©ПИИ·¶ЁөгMөДЧшұкЈ¬ФЩҪбәПөгBөДЧшұкјҙҝЙЗуіцЎчOBMөДГж»эЈ»
ЈЁ3Ј©ПИБӘБўТ»ҙОәҜКэУл·ҙұИАэәҜКэҪвОцКҪЗуіцөгAЧшұкЈ¬ФЩёщҫЭөгPФЪөЪТ»ПуПЮ·ҙұИАэәҜКэЙПЈ¬ҝЙЙиөгPЧшұкОӘЈЁmЈ¬![]() Ј©ЈЁmЈҫ0Ј©Ј¬ҙУ¶шҝЙЦӘөгCөДЧшұкЈ¬ёщҫЭБҪөгЦ®јдөДҫаА빫КҪҝЙЦӘPCЦ®јдөДҫаАлЈ¬ФЩёщҫЭИэҪЗРОөДГж»э№«КҪБРКҪҪвҙрјҙҝЙ.
Ј©ЈЁmЈҫ0Ј©Ј¬ҙУ¶шҝЙЦӘөгCөДЧшұкЈ¬ёщҫЭБҪөгЦ®јдөДҫаА빫КҪҝЙЦӘPCЦ®јдөДҫаАлЈ¬ФЩёщҫЭИэҪЗРОөДГж»э№«КҪБРКҪҪвҙрјҙҝЙ.
ЈЁ1Ј©Ҫ«BЈЁaЈ¬©Ғ4Ј©ҙъИлТ»ҙОәҜКэyЈҪx©Ғ3ЦРөГЈәaЈҪ©Ғ1
ЎаBЈЁ©Ғ1Ј¬©Ғ4Ј©
Ҫ«BЈЁ©Ғ1Ј¬©Ғ4Ј©ҙъИл·ҙұИАэәҜКэ![]() ЦРөГЈәkЈҪ4
ЦРөГЈәkЈҪ4
Ўа·ҙұИАэәҜКэөДұнҙпКҪОӘ![]() Ј»
Ј»
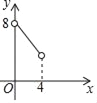
ЈЁ2Ј©УЙТ»ҙОәҜКэyЈҪx©Ғ3ҝЙЦӘЈәMЈЁ3Ј¬0Ј©Ј¬
ЎаOMЈҪ3Ј¬
ЎЯBЈЁ©Ғ1Ј¬©Ғ4Ј©Ј¬
ЎаЎчOBMөДГж»эЈә![]()
ЈЁ3Ј©Ҫв өГ
өГ![]() »т
»т![]() Ј¬
Ј¬
ЎаAЈЁ4Ј¬1Ј©
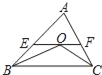
ИзНјЈә

ЙиөгPөДЧшұкОӘЈЁmЈ¬![]() Ј©ЈЁmЈҫ0Ј©Ј¬ФтCЈЁmЈ¬m©Ғ3Ј©
Ј©ЈЁmЈҫ0Ј©Ј¬ФтCЈЁmЈ¬m©Ғ3Ј©
Ўа![]() Ј¬өгOөҪЦұПЯPCөДҫаАлОӘm
Ј¬өгOөҪЦұПЯPCөДҫаАлОӘm
ЎаЎчPOCөДГж»эЈҪ![]()
ҪвөГЈәmЈҪ5»т©Ғ2»т1»т2
ЎЯөгPІ»УлөгAЦШәПЈ¬ЗТAЈЁ4Ј¬1Ј©
ЎаmЎЩ4
УЦЎЯmЈҫ0
ЎаmЈҪ5»т1»т2
ЎаөгPөДЧшұкОӘЈЁ5Ј¬![]() Ј©»тЈЁ1Ј¬4Ј©»тЈЁ2Ј¬2Ј©Ј®
Ј©»тЈЁ1Ј¬4Ј©»тЈЁ2Ј¬2Ј©Ј®

 ГыРЈҝОМГПөБРҙр°ё
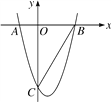
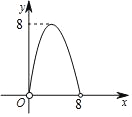
ГыРЈҝОМГПөБРҙр°ёЎҫМвДҝЎҝТСЦӘ¶юҙОәҜКэөДҪвОцКҪКЗyЈҪx2©Ғ2x©Ғ3Ј®
ЈЁ1Ј©УлyЦбөДҪ»өгЧшұкКЗЎЎ ЎЎЈ¬¶ҘөгЧшұкКЗЎЎ ЎЎЈ®
ЈЁ2Ј©ФЪЧшұкПөЦРАыУГГиөг·Ё»ӯіцҙЛЕЧОпПЯЈ»
x | Ўӯ | Ўӯ | |||||
y | Ўӯ | Ўӯ |
ЈЁ3Ј©ҪбәПНјПу»ШҙрЈәөұ©Ғ2ЈјxЈј2КұЈ¬әҜКэЦөyөДИЎЦө·¶О§КЗЎЎ ЎЎЈ®