题目内容
14. 已知等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A.C两点同时出发,均以1cm/s的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.
已知等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A.C两点同时出发,均以1cm/s的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.(1)求出S关于t的函数关系式.
(2)当点P在线段AB上时,点P运动几秒时,S△PCQ=$\frac{1}{4}$S△ABC?
(3)作PE⊥AC于点E,当点P.Q运动时,线段DE的长度是否改变?证明你的结论.
分析 (1)由题可以看出P沿AB向右运动,Q沿BC向上运动,且速度都为1cm/s,S=$\frac{1}{2}$QC×PB,所以求出QC、PB与t的关系式就可得出S与t的关系;
(2)另外应注意P点的运动轨迹,它不仅在B点左侧运动,达到一定时间后会运动到右侧,所以一些问题可能会有两种可能出现的情况,这时我们应分条回答;
(3)根据当t<10秒时,P在线段AB上,得出△APE≌△QCF,以及当t>10秒时,P在线段AB的延长线上,得出DE的长.
解答 解:(1)如图1,过P点作PE⊥AC于E.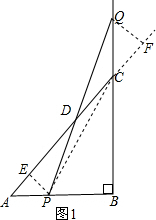 当t<10秒时,P在线段AB上,此时CQ=t,PB=10-t
当t<10秒时,P在线段AB上,此时CQ=t,PB=10-t
∴s=$\frac{1}{2}$×t×(10-t)=$\frac{1}{2}$(10t-t2)
当t>10秒时,P在线段AB得延长线上,此时CQ=t,PB=t-10
∴s=$\frac{1}{2}$×t×(t-10)=$\frac{1}{2}$(t2-10t);
(2)∵S△ABC=$\frac{1}{2}$AB•BC=50,
∴当t<10秒时,S△PCQ=$\frac{1}{2}$(10t-t2)=$\frac{50}{4}$,
整理得t2-10t+25=0,
解得:t=5.
当t>10秒时,S△PCQ=$\frac{1}{2}$(t2-10t)=$\frac{50}{4}$,
整理得t2-10t-25=0解得t=5±5$\sqrt{2}$(舍去负值),
∴当点P运动5秒或5+5$\sqrt{2}$秒时,S△PCQ=$\frac{1}{4}$S△ABC;
(3)当点P,Q运动时,线段DE的长度不会改变.
证明如下:
①当t<10秒时,P在线段AB上,如图1,
过Q作QF⊥AC,交直线AC于点F
,在Rt△APE和Rt△QCF中,
$\left\{\begin{array}{l}{∠AEP=∠QFC}\\{∠A=∠QCF}\\{AP=QC}\end{array}\right.$,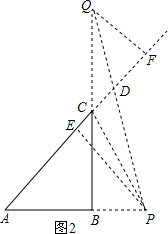 ∴△APE≌△QCF,
∴△APE≌△QCF,
∴AE=PE=CF=QF=$\frac{\sqrt{2}}{2}$t,
∴四边形PEQF是平行四边形,且DE是对角线EF的一半
又∵EF=AC=10$\sqrt{2}$,
∴DE=5$\sqrt{2}$,
②当t>10秒时,P在线段AB的延长线上,如图2,
作PE⊥AC,交直线AC于点E,过Q作QF⊥AC,交直线AC于点F.
同理可得DE=5$\sqrt{2}$.
∴当点P、Q运动时,线段DE的长度不会改变.
点评 此题主要考查了平行四边形的判定与性质,根据已知分别进行讨论当t<10秒以及当t>10秒是解题关键.

 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案| A. | ±4 | B. | 4 | C. | ±2 | D. | 2 |
①0.000126=1.26×10-4;②3.10×104=31000;
③1.1×10-5=0.000011;④12600000=1.26×106.
| A. | ①② | B. | ②④ | C. | ①②③ | D. | ①③④ |
| A. | 摸出一个红球的可能性大 | B. | 摸出一个白球的可能性大 | ||
| C. | 两种可能性一样大 | D. | 无法确定 |
 如图,一艘客轮在大平洋中航行,所在位置是A(140°,20°),10小时后到达B地,用坐标表示B地的位置是(120°,30°).
如图,一艘客轮在大平洋中航行,所在位置是A(140°,20°),10小时后到达B地,用坐标表示B地的位置是(120°,30°).