题目内容
6.一个黑色不透明的袋子里装有除颜色外其余都相同的7个红球和3个白球,那么从这个袋子中摸出一个红球的可能性和摸出一个白球的可能性相比( )| A. | 摸出一个红球的可能性大 | B. | 摸出一个白球的可能性大 | ||
| C. | 两种可能性一样大 | D. | 无法确定 |
分析 根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
解答 解:∵袋子里装有除颜色外其余都相同的7个红球和3个白球,
∴总球数是10,
∴从这个袋子中摸出一个红球的可能性是$\frac{7}{10}$,摸出一个白球的可能性是$\frac{3}{10}$,
∴从这个袋子中摸出一个红球的可能性和摸出一个白球的可能性相比摸出一个红球的可能性大;
故选:A.
点评 本题主要考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
17.在下列各对单项式中,不是同类项的是( )
| A. | -mn与2mn | B. | -1与0 | C. | $-\frac{{32x{y^2}}}{5}$与xy2 | D. | -$\frac{1}{5}$a2bc与$\frac{1}{5}$a2b |
11.以下列各组线段为边长,能构成直角三角形的是( )
| A. | 1,1,$\sqrt{3}$ | B. | 3,4,5 | C. | 5,10,13 | D. | 2,3,4 |
15.一个不透明的口袋中装有3个红球和12个黄球,这些球除了颜色外,无其他差别,从中随机摸出一个球,恰好是红球的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{4}{5}$ |
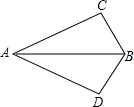 如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要加条件BC=BD或AC=AD.
如图,在△ABC和△ABD中,∠C=∠D=90°,若利用“HL”证明△ABC≌△ABD,则需要加条件BC=BD或AC=AD. 已知等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A.C两点同时出发,均以1cm/s的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.
已知等腰直角△ABC的直角边AB=BC=10cm,点P,Q分别从A.C两点同时出发,均以1cm/s的相同速度作直线运动,已知P沿射线AB运动,Q沿边BC的延长线运动,PQ与直线AC相交于点D.设P点运动时间为t,△PCQ的面积为S.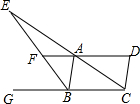 在?ABCD中,∠ABC的外角∠ABG的平分线BE分别交DA,CA的延长线于点F、E.
在?ABCD中,∠ABC的外角∠ABG的平分线BE分别交DA,CA的延长线于点F、E.