题目内容
16.已知$\frac{(2a-b)^{2}+\sqrt{|a|-5}}{\sqrt{a+5}}$=0,求:($\sqrt{a}$+2$\sqrt{b}$)($\sqrt{a}$-2$\sqrt{b}$)的值.分析 先根据非负数的性质求出a、b的值,再分别代入即可解决问题.
解答 解:原式=a-4b.
∵$\frac{(2a-b)^{2}+\sqrt{|a|-5}}{\sqrt{a+5}}$=0,
又∵(2a-b)2≥0,$\sqrt{|a|-5}$≥0,
∴$\left\{\begin{array}{l}{2a-b=0}\\{a=±5}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=5}\\{b=10}\end{array}\right.$或$\left\{\begin{array}{l}{a=-5}\\{b=-10}\end{array}\right.$,
∴当a=5,b=10时,原式=5-40=-35,
当a=-5,b=-10时,原式=-5+40=35.
点评 本题考查二次根式的化简求值、非负数的性质等知识,解题的关键是熟练掌握二次根式混合运算的法则,学会应用非负数性质解决问题,属于中考常考题型.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
4.方程x2+4x-4=0的左边配成完全平方后所得的方程为( )
| A. | (x+2)2=8 | B. | (x-2)2=8 | C. | (x+2)2=4 | D. | (x-2)2=4 |
6.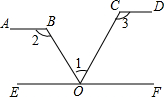 如图,AB∥CD∥EF,下列各式中,正确的是( )
如图,AB∥CD∥EF,下列各式中,正确的是( )
 如图,AB∥CD∥EF,下列各式中,正确的是( )
如图,AB∥CD∥EF,下列各式中,正确的是( )| A. | ∠1+∠2+∠3=180° | B. | ∠1+∠2-∠3=90° | C. | ∠1-∠2+∠3=90° | D. | ∠2+∠3-∠1=180° |
 将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEB′=$\frac{2}{5}$∠AEB′,则∠AEB′=75°.
将长方形ABCD沿AE折叠,得到如图所示的图形,已知∠CEB′=$\frac{2}{5}$∠AEB′,则∠AEB′=75°. 如图,矩形纸片ABCD,用如下方法折叠该纸片:
如图,矩形纸片ABCD,用如下方法折叠该纸片: 如图,当∠1=∠3时,AB∥CD.
如图,当∠1=∠3时,AB∥CD.