题目内容
14．一次函数y=mx+2的图象与x轴交于点（-2，0），则m=1．分析 把点的坐标代入一次函数解析式可求得m的值．
解答 解：
∵y=mx+2的图象与x轴交于点（-2，0），
∴把点的坐标代入解析式可得0=-2m+2，解得m=1，
故答案为：1．
点评 本题主要考查函数图象上点的坐标与函数解析式的关系，掌握图象上点的坐标满足函数解析式是解题的关键．
练习册系列答案
相关题目
4．在有25名男生和24名女生的班级中，随机抽签确定一名学生代表，则下列说法正确的是（ ）
| A． | 男、女生做代表的可能性一样大 | |
| B． | 男生做代表的可能性较大 | |
| C． | 女生做代表的可能性较大 | |
| D． | 男、女生做代表的可能性的大小不能确定 |
2．在二次根式$\sqrt{20a}$，a$\sqrt{2a}$，$\sqrt{\frac{a}{2}}$，$\sqrt{{a}^{2}+{b}^{2}}$中，最简二次根式有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
9．
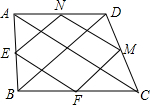在四边形ABCD中，连接对角线AC，BD，E、F、M、N分别是AB、BC、CD、AD的中点，连接EF、FM、MN、EN，下列条件中，能使四边形EFMN是菱形的是（ ）
在四边形ABCD中，连接对角线AC，BD，E、F、M、N分别是AB、BC、CD、AD的中点，连接EF、FM、MN、EN，下列条件中，能使四边形EFMN是菱形的是（ ）| A． | AB=BC | B． | AB⊥BC | C． | AC⊥BD | D． | AC=BD |
如图，矩形ABCD中，点E、F分别是AB、CD的中点，连接DE和BF，分别取DE、BF的中点M、N，连接AM、CN、MN．若AB=3$\sqrt{2}$，BC=2$\sqrt{3}$，则图中阴影部分的面积为3$\sqrt{6}$．
3．若a＞b，则下列式子正确的是（ ）
| A． | -5a＞-5b | B． | a-3＞b-3 | C． | 4-a＞4-b | D． | $\frac{1}{2}$a＜$\frac{1}{2}$b |
．