题目内容
6. 如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3$\sqrt{2}$,BC=2$\sqrt{3}$,则图中阴影部分的面积为3$\sqrt{6}$.
如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM、CN、MN.若AB=3$\sqrt{2}$,BC=2$\sqrt{3}$,则图中阴影部分的面积为3$\sqrt{6}$.
分析 根据矩形的中心对称性判定阴影部分的面积等于空白部分的面积,从而得到阴影部分的面积等于矩形的面积的一半,再根据矩形的面积公式即可得解.
解答 解:∵点E、F分别是AB、CD的中点,M、N分别为DE、BF的中点,
∴矩形绕中心旋转180°阴影部分恰好能够与空白部分重合,
∴阴影部分的面积等于空白部分的面积,
∴阴影部分的面积=$\frac{1}{2}$矩形的面积=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×3$\sqrt{2}$×2$\sqrt{3}$=3$\sqrt{6}$;
故答案为:3$\sqrt{6}$.
点评 本题考查了矩形的性质,主要利用了矩形的中心对称性,判断出阴影部分的面积等于矩形的面积的一半是解题的关键.

练习册系列答案
相关题目
16. 如图,直线l上有三个正方形a、b、c,点c在l上,若a、c的面积分别为5和11,则b的面积为( )
如图,直线l上有三个正方形a、b、c,点c在l上,若a、c的面积分别为5和11,则b的面积为( )
 如图,直线l上有三个正方形a、b、c,点c在l上,若a、c的面积分别为5和11,则b的面积为( )
如图,直线l上有三个正方形a、b、c,点c在l上,若a、c的面积分别为5和11,则b的面积为( )| A. | 16 | B. | 18 | C. | 25 | D. | 45 |
17.在学校组织的社会实践活动中,甲、乙两人参加了射击比赛,每人射击七次,命中的环数如表:
根据以上信息,解决一下问题:
(1)写出甲、乙两人命中环数的众数;
(2)已知通过计算器求得$\overline{{x}_{甲}}$=8,s甲2≈1.43,试比较甲、乙两人谁的成绩更稳定?
| 序号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 甲命中的环数(环) | 7 | 8 | 8 | 6 | 9 | 8 | 10 |
| 乙命中的环数(环) | 5 | 10 | 6 | 7 | 8 | 10 | 10 |
(1)写出甲、乙两人命中环数的众数;
(2)已知通过计算器求得$\overline{{x}_{甲}}$=8,s甲2≈1.43,试比较甲、乙两人谁的成绩更稳定?
18.如图,∠1+∠B=180°,∠2=45°,则∠D的度数是( )


| A. | 25° | B. | 45° | C. | 50° | D. | 65° |
 如图,已知AC垂直平分BD,∠ABC=∠DAF,DF⊥BD
如图,已知AC垂直平分BD,∠ABC=∠DAF,DF⊥BD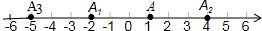 如图,数轴上,点A的初始位置表示的数为1,现A做如下移动:第1次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,对于点An,当n=2015时,这个点表示的数是-3023.
如图,数轴上,点A的初始位置表示的数为1,现A做如下移动:第1次点A向左移动3个单位长度至点A1,第2次从点A1向右移动6个单位长度至点A2,第3次从点A2向左移动9个单位长度至点A3,…,按照这种移动方式进行下去,对于点An,当n=2015时,这个点表示的数是-3023. 中,自变量
中,自变量 的取值范围是 .
的取值范围是 .